生存分析的Cox回归模型(比例风险模型)R语言实现及结果解读
R语言中的Cox模型分析
单变量Cox回归
library("survival")
library("survminer")
res.cox <- coxph(Surv(time, status) ~ sex, data = lung)
summary(res.cox)
res.cox <- coxph(Surv(time, status) ~ sex, data = lung)
summary(res.cox)
summary的结果:
Call:
coxph(formula = Surv(time, status) ~ sex, data = lung)
n= 228, number of events= 165
coef exp(coef) se(coef) z Pr(>|z|)
sex -0.5310 0.5880 0.1672 -3.176 0.00149 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
exp(coef) exp(-coef) lower .95 upper .95
sex 0.588 1.701 0.4237 0.816
Concordance= 0.579 (se = 0.021 )
Likelihood ratio test= 10.63 on 1 df, p=0.001
Wald test = 10.09 on 1 df, p=0.001
Score (logrank) test = 10.33 on 1 df, p=0.001
Cox回归结果可以解释如下:
统计显着性。标记为“z”的列给出了Wald统计值。它对应于每个回归系数与其标准误差的比率(z = coef / se(coef))。wald统计评估是否beta(ββ)系数在统计上显着不同于0。从上面的输出,我们可以得出结论,变量性别具有高度统计学意义的系数。
回归系数。Cox模型结果中要注意的第二个特征是回归系数(coef)的符号。一个积极的信号意味着危险(死亡风险)较高,因此对于那些变量值较高的受试者,预后更差。变量性别编码为数字向量。1:男,2:女。Cox模型的R总结给出了第二组相对于第一组,即女性与男性的风险比(HR)。性别的β系数= -0.53表明在这些数据中,女性的死亡风险(低存活率)低于男性。
危害比例。指数系数(exp(coef)= exp(-0.53)= 0.59)也称为风险比,给出协变量的效应大小。例如,女性(性别= 2)将危害降低了0.59倍,即41%。女性与预后良好相关。
风险比的置信区间。总结结果还给出了风险比(exp(coef))的95%置信区间的上限和下限,下限95%界限= 0.4237,上限95%界限= 0.816。
全球统计学意义的模型。最后,输出为模型的总体显着性提供了三个替代测试的p值:可能性比率测试,Wald测试和得分logrank统计。这三种方法是渐近等价的。对于足够大的N,他们会得到相似的结果。对于小N来说,它们可能有所不同。似然比检验对于小样本量具有更好的表现,所以通常是优选的。
批量单变量cox分析
covariates <- c("age", "sex", "ph.karno", "ph.ecog", "wt.loss")
univ_formulas <- sapply(covariates,
function(x) as.formula(paste('Surv(time, status)~', x)))
univ_models <- lapply( univ_formulas, function(x){coxph(x, data = lung)})
# Extract data
univ_results <- lapply(univ_models,
function(x){
x <- summary(x)
p.value<-signif(x$wald["pvalue"], digits=2)
wald.test<-signif(x$wald["test"], digits=2)
beta<-signif(x$coef[1], digits=2);#coeficient beta
HR <-signif(x$coef[2], digits=2);#exp(beta)
HR.confint.lower <- signif(x$conf.int[,"lower .95"], 2)
HR.confint.upper <- signif(x$conf.int[,"upper .95"],2)
HR <- paste0(HR, " (",
HR.confint.lower, "-", HR.confint.upper, ")")
res<-c(beta, HR, wald.test, p.value)
names(res)<-c("beta", "HR (95% CI for HR)", "wald.test",
"p.value")
return(res)
#return(exp(cbind(coef(x),confint(x))))
})
res <- t(as.data.frame(univ_results, check.names = FALSE))
as.data.frame(res)
beta HR (95% CI for HR) wald.test p.value age 0.019 1 (1-1) 4.1 0.042 sex -0.53 0.59 (0.42-0.82) 10 0.0015 ph.karno -0.016 0.98 (0.97-1) 7.9 0.005 ph.ecog 0.48 1.6 (1.3-2) 18 2.7e-05 wt.loss 0.0013 1 (0.99-1) 0.05 0.83
多变量Cox回归
要一次性将单变量coxph函数应用于多个协变量,请输入:
res.cox <- coxph(Surv(time, status) ~ age + sex + ph.ecog, data = lung)
summary(res.cox)
Call:
coxph(formula = Surv(time, status) ~ age + sex + ph.ecog, data = lung)
n= 227, number of events= 164
(1 observation deleted due to missingness)
coef exp(coef) se(coef) z Pr(>|z|)
age 0.011067 1.011128 0.009267 1.194 0.232416
sex -0.552612 0.575445 0.167739 -3.294 0.000986 ***
ph.ecog 0.463728 1.589991 0.113577 4.083 4.45e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
exp(coef) exp(-coef) lower .95 upper .95
age 1.0111 0.9890 0.9929 1.0297
sex 0.5754 1.7378 0.4142 0.7994
ph.ecog 1.5900 0.6289 1.2727 1.9864
Concordance= 0.637 (se = 0.025 )
Likelihood ratio test= 30.5 on 3 df, p=1e-06
Wald test = 29.93 on 3 df, p=1e-06
Score (logrank) test = 30.5 on 3 df, p=1e-06
所有3个整体测试(可能性,Wald 和 得分)的p值都是显着的,表明该模型是显着的。这些测试评估了所有的beta(ββ)为0.在上面的例子中,检验统计是完全一致的,综合零假设被完全拒绝。
在多变量Cox分析中,协变量性别和ph.ecog仍然显着(p <0.05)。然而,协变量年龄并不显着(P = 0.17,这比0.05)。
性别p值为0.000986,危险比HR = exp(coef)= 0.58,表明患者性别和死亡风险降低之间有很强的关系。协变量的风险比可以解释为对风险的倍增效应。例如,保持其他协变量不变,女性(性别= 2)将危害降低0.58倍,即42%。我们的结论是,女性与良好的预后相关。
类似地,ph.ecog的p值是4.45e-05,危险比HR = 1.59,表明ph.ecog值与死亡风险增加之间的强关系。保持其他协变量不变,ph.ecog值越高,生存率越差。
相比之下,年龄的p值现在是p = 0.23。风险比HR = exp(coef)= 1.01,95%置信区间为0.99至1.03。由于HR的置信区间为1,这些结果表明,年龄在调整了ph值和患者性别后对HR的差异的贡献较小,并且仅趋向显着性。例如,保持其他协变量不变,额外的年龄会导致每日死亡危险因素为exp(beta)= 1.01或1%,这不是一个重要的贡献。
可视化估计的生存时间分布
已经将Cox模型拟合到数据中,可以在特定风险组的任何给定时间点可视化预测的存活比例。函数survfit()估计生存比例,默认情况下为协变量的平均值。
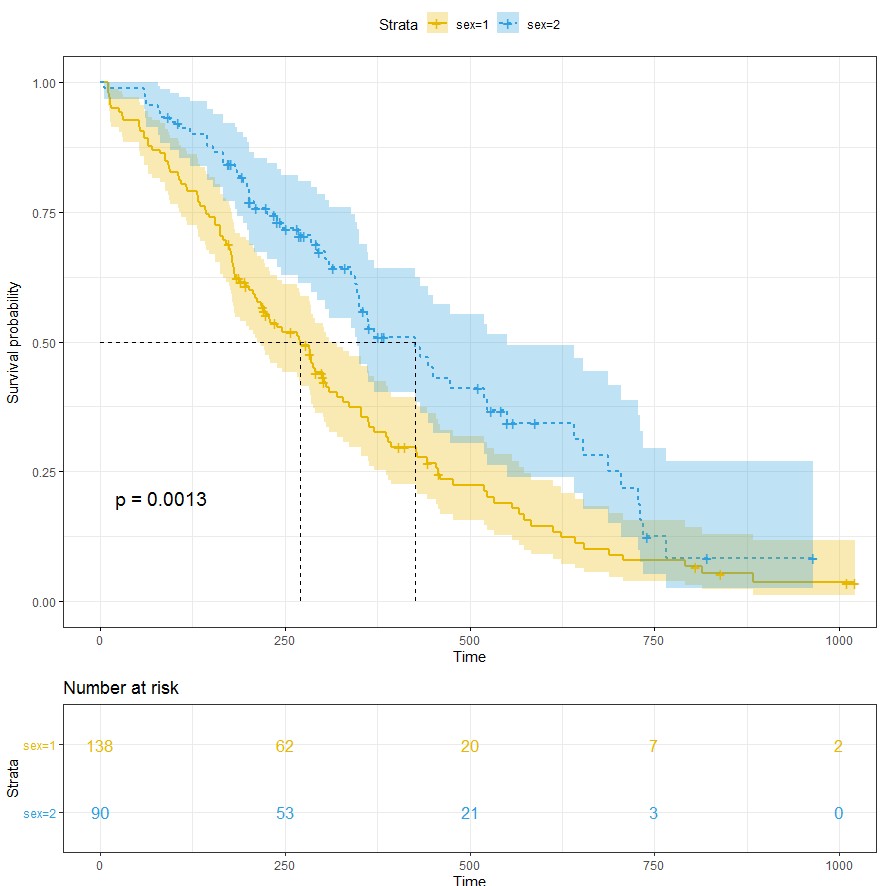
绘制生存曲线:
kmfit<-survfit(Surv(time, status) ~ sex, data = lung)
ggsurvplot(kmfit,
pval = TRUE, conf.int = TRUE,
risk.table = TRUE,
risk.table.col = "strata",
linetype = "strata",
surv.median.line = "hv",
ggtheme = theme_bw(),
palette = c("#E7B800", "#2E9FDF"))
更多生物信息课程:
1. 文章越来越难发?是你没发现新思路,基因家族分析发2-4分文章简单快速,学习链接:基因家族分析实操课程、基因家族文献思路解读
2. 转录组数据理解不深入?图表看不懂?点击链接学习深入解读数据结果文件,学习链接:转录组(有参)结果解读;转录组(无参)结果解读
3. 转录组数据深入挖掘技能-WGCNA,提升你的文章档次,学习链接:WGCNA-加权基因共表达网络分析
4. 转录组数据怎么挖掘?学习链接:转录组标准分析后的数据挖掘、转录组文献解读
5. 微生物16S/ITS/18S分析原理及结果解读、OTU网络图绘制、cytoscape与网络图绘制课程
6. 生物信息入门到精通必修基础课:linux系统使用、perl入门到精通、perl语言高级、R语言画图
7. 医学相关数据挖掘课程,不用做实验也能发文章:TCGA-差异基因分析、GEO芯片数据挖掘、 GEO芯片数据不同平台标准化 、GSEA富集分析课程、TCGA临床数据生存分析、TCGA-转录因子分析、TCGA-ceRNA调控网络分析
8.其他,二代测序转录组数据自主分析、NCBI数据上传、二代测序数据解读、
9.更多课程可点击:组学大讲堂视频课程
- 发表于 2019-12-06 20:29
- 阅读 ( 26320 )
- 分类:TCGA
你可能感兴趣的文章
相关问题
- 请教一下TCGA的蛋白数据怎么理解,它是有正负值的,这个正负值代表什么意思,为什么蛋白表达会有负值?我只想给它分成高表达,低表达和表达缺失组应该怎么处理呀? 0 回答
- TCGA下载 docker报错 0 回答
- TCGA差异分析如何根据临床信息分组? 1 回答
- TCGA用R数据下载错误 1 回答
- 老师,想请教一下TCGA基因表达数据的问题,我从xena.ucsc网页上下载了基因表达数据TCGA-CESC.htseq_counts.tsv;然后发现该数据中只有Ensembl格式的基因ID ,没有SYMBOL格式的。所以接下来进行基因ID格式转换,却发现同一个SYMBOL ID对应的多个Ensembl格式的ID,想问下老师,这种情况该怎么处理?同一个SYMBOL ID所对应的多个Ensembl格式ID的基因表达数据应该留下哪一个? 1 回答
- TCGA的RNA-seq count annotation过滤,有些不知道是否需要删除 0 回答
