R语言-Cox比例风险模型
Cox比例风险模型(cox proportional-hazards model),简称Cox模型
是由英国统计学家D.R.Cox(1972)年提出的一种半参数回归模型。该模型以生存结局和生存时间为应变量,可同时分析众多因素对生存期的影响,能分析带有截尾生存时间的资料,且不要求估计资料的生存分布类型
Cox模型的基本假设为:
在任意一个时间点,两组人群发生时间的风险比例是恒定的;或者说其危险曲线应该是成比例而且是不能交叉的;也就是如果一个体在某个时间点的死亡风险是另外一个体的两倍,那么在其他任意时间点的死亡风险也同样是2倍 总之,Cox模型的协变量(变量因素)参数必须满足上述假设,但是有时在研究过程中会遇到延迟反应、假性进展,从而导致生存曲线(如PFS)早期就纠缠在一起,几个月后才分开,这在免疫疗法中会遇到免疫治疗困局:COX模型不符合等比例风险假设怎么办?,这时Cox模型的假设就不成立了
如果事件的终点不止一个,即存在多个终点并同时竞争风险,那么Cox模型也是不适用了,一般这时会考虑适用竞争风险模型,而这些终点事件互被称为竞争风险事件
Cox模型与Kaplan-Meier法:
- Kaplan-Meier法是非参数法,而Cox模型是半参数法,一般来说在符合一定条件下,后者的检验效应要大于前者
- Kaplan-Meier法一般处理单因素对研究生存结局的影响,而Cox模型可以同时处理多个因素对生存结局的影响
Cox模型可以由hazard function表示,h(t);简单的说就是t时刻死亡的风险,公式如下:
h(t)=h0(t) × exp(b1x1 + b2x2 +...+ bpxp)
- t代表生存时间
- x1-xp代表协变量
- b1-bp代表协变量的回归系数
接着如何在R中计算Cox模型
同样还是用到以下两个包:
library("survival")
library("survminer")
计算Cox模型主要用到的是coxph()函数,但需要先用Surv()函数产生一个生存对象;另外coxph()函数支持的方法有:exact,breslow以及exact,默认是exact
以lung数据集为例,看下性别因素对生存结局的影响
data("lung")
res.cox <- coxph(Surv(time, status) ~ sex, data = lung)
> summary(res.cox)
Call:
coxph(formula = Surv(time, status) ~ sex, data = lung)
n= 228, number of events= 165
coef exp(coef) se(coef) z Pr(>|z|)
sex -0.5310 0.5880 0.1672 -3.176 0.00149 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
exp(coef) exp(-coef) lower .95 upper .95
sex 0.588 1.701 0.4237 0.816
Concordance= 0.579 (se = 0.022 )
Rsquare= 0.046 (max possible= 0.999 )
Likelihood ratio test= 10.63 on 1 df, p=0.001
Wald test = 10.09 on 1 df, p=0.001
Score (logrank) test = 10.33 on 1 df, p=0.001
上述summary结果中的coef就是公式中的回归系数b(有时也叫做beta值),因此exp(coef)则是Cox模型中最主要的概念风险比(HR-hazard ratio):
- HR = 1: No effect
- HR < 1: Reduction in the hazard
- HR > 1: Increase in Hazard
在癌症研究中:
- hazard ratio > 1 is called bad prognostic factor
- hazard ratio < 1 is called good prognostic factor
z(-3.176)值代表Wald统计量,其值等于回归系数coef除以其标准误se(coef),即z = coef/se(coef);有统计量必有其对应的假设检验的显著性P值(0.00149),其说明bata值是否与0有统计学意义上的显著差别
coef(-0.5310)值小于0说明HR值小于1,而这里的Cox模型是group two相对于group one而言的,那么按照测试数据集来说:male=1,female=1,即女性的死亡风险相比男性要低
exp(coef)等于0.59,即风险比例等于0.59,说明女性(male=2)减少了0.59倍风险,女性与良好预后相关
lower .95 upper .95则是exp(coef)的95%置信区间
Likelihood ratio test,Wald test,Score (logrank) test则是给出了3种可选择的P值,这三者是asymptotically equivalent;当样本数目足够大时(我也不知道多少样本是足够大。。),这三者的值是相似的;当样本数目较少时,这三者是有差别的,但是Likelihood ratio test会比其他两种在小样本中表现的更优
Cox模型在于其可以对多因素进行Cox回归分析,如我们想同时考虑年龄、性别以及ECOG performance score(ph.ecog)对生存结局的影响
res.cox <- coxph(Surv(time, status) ~ age + sex + ph.ecog, data = lung)
> summary(res.cox)
Call:
coxph(formula = Surv(time, status) ~ age + sex + ph.ecog, data = lung)
n= 227, number of events= 164
(1 observation deleted due to missingness)
coef exp(coef) se(coef) z Pr(>|z|)
age 0.011067 1.011128 0.009267 1.194 0.232416
sex -0.552612 0.575445 0.167739 -3.294 0.000986 ***
ph.ecog 0.463728 1.589991 0.113577 4.083 4.45e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
exp(coef) exp(-coef) lower .95 upper .95
age 1.0111 0.9890 0.9929 1.0297
sex 0.5754 1.7378 0.4142 0.7994
ph.ecog 1.5900 0.6289 1.2727 1.9864
Concordance= 0.637 (se = 0.026 )
Rsquare= 0.126 (max possible= 0.999 )
Likelihood ratio test= 30.5 on 3 df, p=1e-06
Wald test = 29.93 on 3 df, p=1e-06
Score (logrank) test = 30.5 on 3 df, p=1e-06
这里的结果形式大致上跟单因素的一样,我们主要需要看的是以下几点:
Likelihood ratio test/Wald test/Score (logrank) test三种假设检验方法给出的P值说明Cox模型对三个因素均进行了beta值是否为0的假设检验,并且拒绝了omnibus null hypothesis(beta=0的零假设)
该模型结果给出了三个因素各自在其他因素保持不变下的HR以及P值;比如年龄因素的HR=1.01以及P=0.23,说明年龄因素在调整了性别和ph.ecog因素的影响后,其对HR的变化贡献较小(只有1%)
而看性别因素,HR=0.58,以及P=0.000986,说明在保持其他因素不变的情况下,年龄和死亡风险有很强的关系,女性能将死亡风险降低0.58倍,再次说明了女性与良好预后相关
最后看下生存曲线
根据数据拟合的Cox模型,我们可以将其在各个时间的预测的生存比例进行可视化展示。使用survfit()函数评估生存比例,默认是依据所有因素(协变量)的平均值
ggsurvplot(survfit(res.cox), data = lung, palette = "#2E9FDF",
ggtheme = theme_minimal(), legend = "none")
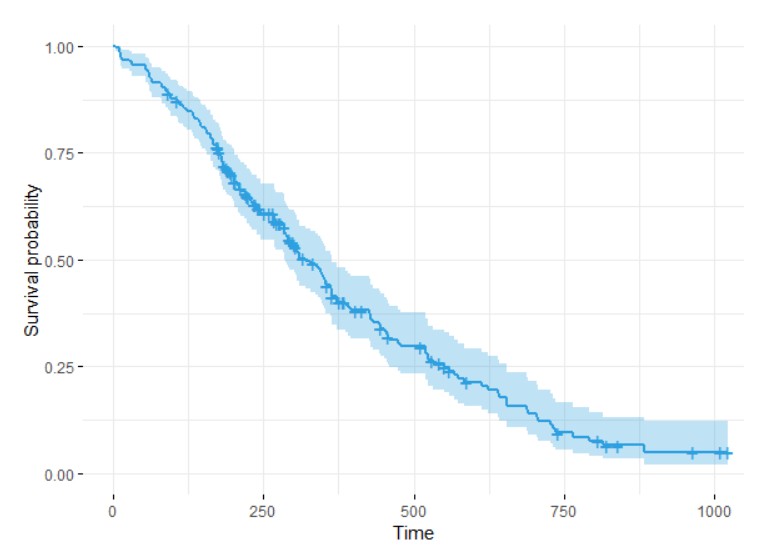
Cox_model
如果想单独看一下上面这个Cox模型中某个因素(协变量)的预测可视化图,教程中则是将其他两个因素(协变量)做些处理:
In this case, we construct a new data frame with two rows, one for each value of sex; the other covariates are fixed to their average values (if they are continuous variables) or to their lowest level (if they are discrete variables). For a dummy covariate, the average value is the proportion coded 1 in the data set
代码照搬下:
# Create the new data
sex_df <- with(lung,
data.frame(sex = c(1, 2),
age = rep(mean(age, na.rm = TRUE), 2),
ph.ecog = c(1, 1)
)
)
fit <- survfit(res.cox, newdata = sex_df)
ggsurvplot(fit, data = sex_df, conf.int = TRUE,
legend.labs=c("Sex=1", "Sex=2"),
ggtheme = theme_minimal())
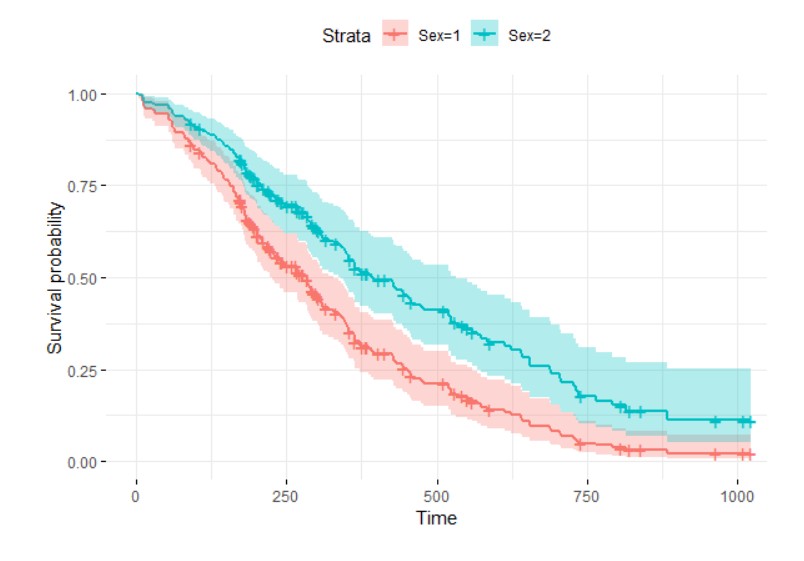
Cox_model_2
主要参考资料:
Cox Proportional-Hazards Model
生存分析函数小结
本文出自于http://www.bioinfo-scrounger.com转载请注明出处
- 发表于 2021-05-14 13:53
- 阅读 ( 4198 )
- 分类:R
你可能感兴趣的文章
- univariate_cox.r 临床数据单因素cox回归分析 4650 浏览
- multi_cox.r 基因表达量做多因素cox分析 4957 浏览
- cox模型评估-决策曲线分析(DCA) 15742 浏览
- lasso_cox.r lasso_cox 模型优化分析 6654 浏览
- univariate_cox_batch.r 基因表达量批量单因素cox回归分析 4188 浏览
