Rtsne包降维聚类分析
Rtsne包降维聚类分析
t-SNE优缺点
优点
对于不相似的点，用一个较小的距离会产生较大的梯度来让这些点排斥开来。
这种排斥又不会无限大(梯度中分母)，避免不相似的点距离太远。
缺点
主要用于可视化，很难用于其他目的。
t-SNE倾向于保存局部特征，对于本征维数(intrinsic dimensionality)本身就很高的数据集，是不可能完整的映射到2-3维的空间
全局结构未明确保留。这个问题可以通过PCA初始化点（使用init ='pca'）来缓解。
计算量大，耗时间是PCA的百倍，内存占用大。
应用
1、识别肿瘤亚群（医学成像）
质谱成像（MSI）是一种同时提供组织中数百个生物分子的空间分布的技术。t-SNE，通过数据的非线性可视化，能够更好地解析生物分子肿瘤内异质性。
2、 人脸识别
人脸识别技术已经取得巨大进展，很多诸如PCA之类的算法也已经在该领域被研究过。但是由于降维和分类的困难，人脸识别依然具有挑战性。t-SNE被用于高维度数据降维，然后用其它算法，例如 AdaBoostM2, 随机森林, 逻辑回归, 神经网络等多级分类器做表情分类。
R语言实现
Rtsne包
主要参数
| dims | 参数设置降维之后的维度，默认是2 |
| perplexity | 困惑度，参数须取值小于(nrow(data)-1)/3 |
| theta | 参数越大，结果的准确度越低，默认是0.5 |
| max_iter | 最大迭代次数 |
| pca | 表示是否对输入的原始数据进行PCA分析，然后用分析后的数据进行后续分析，一般选择TRUE |
library(Rtsne)
iris_unique <- unique(iris) #去重复
tsne_out <- Rtsne(as.matrix(iris_unique[,1:4])) #运行t-SNE
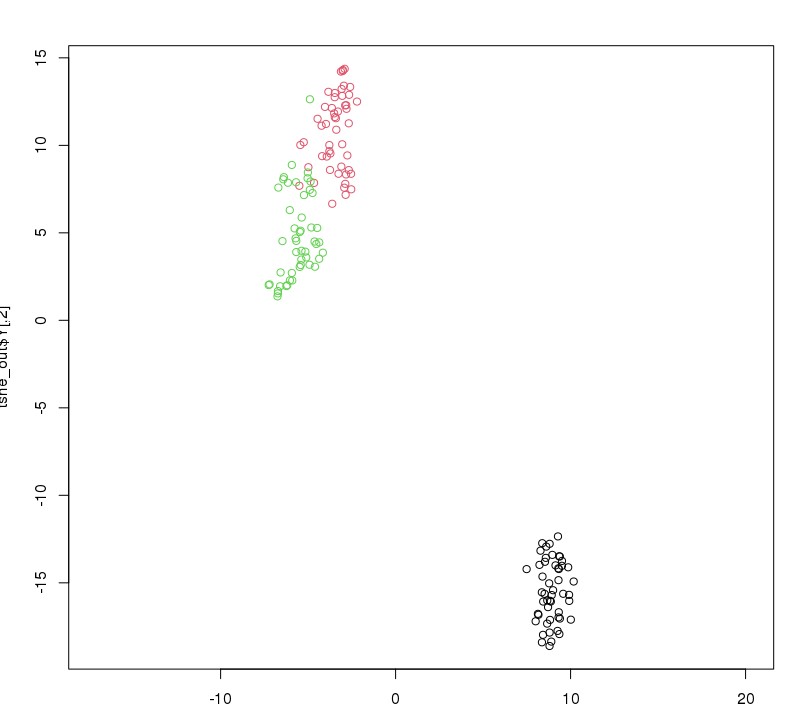
plot(tsne_out$Y,col=iris$Species,asp=1) #asp 限定 aspect 比率
- 发表于 2021-05-24 15:37
- 阅读 ( 2397 )
- 分类：R
