微生物组间差异分析之LEfSe
LEfSe分析，可以分析组间菌群差异，找出各组间差异的微生物种类，有助于开发biomaker等研究，因此LEfSe分析在微生物相关文章中经常出现。我们今天来详细讲解一下LEfSe分析的原理及图表解读。
LEfSe分析原理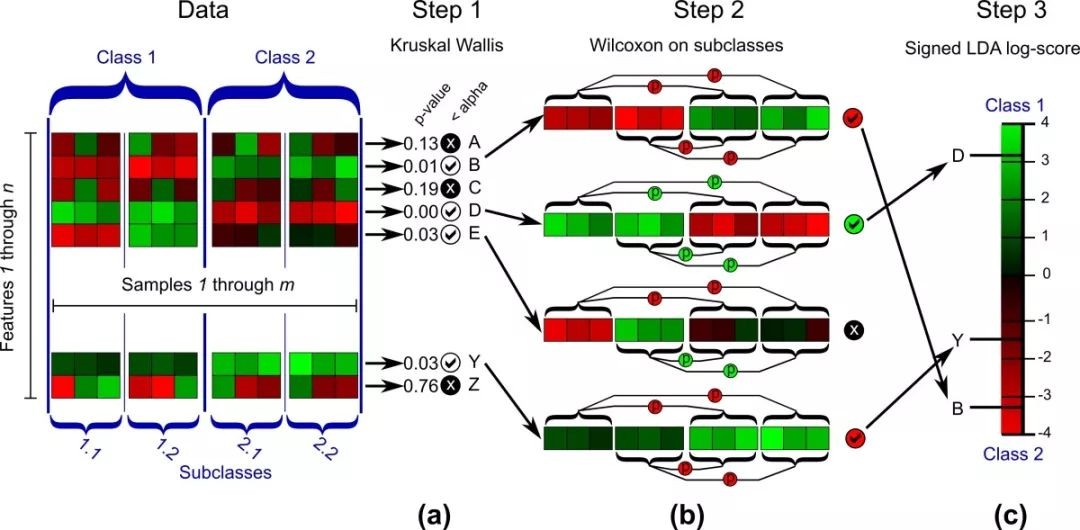
运行LEfSe软件主要分三大步骤：第一步：需要把普通的物种、基因等等的丰度信息的表格转化成LEfSe识别的格式。这一步会生成.in结尾的文件
第二步：这一步也是最关键的一步，统计显著差异的biomarker、统计子组组间差异、统计effect sizes（LDA score），会生成.res格式的文件。如下图所示
Step1：两组或两组以上的样本中采用的非参数因子Kruskal-Wallis秩和检验检测出biomarker。
Step2：基于上步的显著差异物种基因，进行两两组之间的Wilcoxon秩和检验，检测出组间差异。
Step3：线性判别分析（LDA）对biomarker进行评估差异显著的物种的影响力（即LDA score），最终获得biomarker。
第三步：基于第二大步的数据，绘制各种图片。
前两步的Kruskal-Wallis秩和检验、Wilcoxon秩和检验 比较简单，类似T检验或者方差检验等，只不过T检验和方差分析为参数检验（要求数据符合方差齐性、正态分布），而在微生物多样性分析中，样品物种丰度分布不确定，多采用非参数检验，所以采用非参数的Kruskal-Wallis秩和检验、Wilcoxon秩和检验。比较复杂一点的就是最后的LDA分析。
LDA是一种监督学习的降维技术，也就是说其数据集中的每个样本是有类别输出的。是在目前机器学习、数据挖掘领域经典且热门的一个算法这点和PCA不同。PCA是不考虑样本类别输出的无监督降维技术。LDA是有监督的，所以LDA算法可以很好的利用样本的分组信息，得到的结果更可靠，这就是LDA分析优势。理解了LDA分析的原理，就不难理解LEfSe的分析结果了。
LDA分析原理：
LDA是一种经典的降维方法线性判别分析（Linear Discriminant Analysis）。LDA的思想可以用一句话概括，就是“投影后类内方差最小，类间方差最大”。什么意思呢？ 我们要将数据在低维度上进行投影，投影后希望每一种类别数据的投影点尽可能的接近，而不同类别的数据的类别中心之间的距离尽可能的大。
可能还是有点抽象，我们先看看最简单的情况。假设我们有两类数据 分别为红色和蓝色，如下图所示，这些数据特征是二维的，我们希望将这些数据投影到一维的一条直线，让每一种类别数据的投影点尽可能的接近，而红色和蓝色数据中心之间的距离尽可能的大。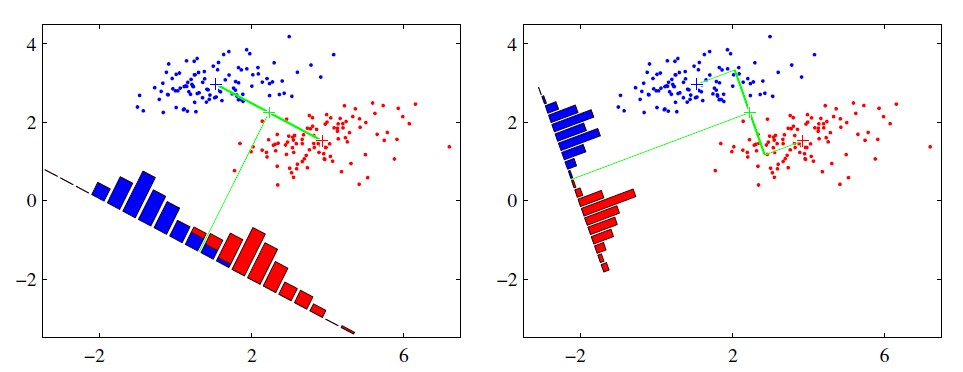
上图中提供了两种投影方式，哪一种能更好的满足我们的标准呢？从直观上可以看出，右图要比左图的投影效果好。因为右图的黑色数据和蓝色数据各个较为集中，且类别之间的距离明显，而左图则在边界处数据混杂。以上就是LDA的主要思想了，当然在实际应用中，我们的数据是多个类别的，我们的原始数据一般也是超过二维的，投影后的也一般不是直线，而是一个低维的超平面。
LEfSe分析结果：LDA值分布柱状图：
图中展示了LDA Score大于设定值的物种(less_strict 设为2；more_strict 设为4)，即组间具有统计学差异的Biomarker。展示了不同组中丰度差异显著的物种，柱状图的长度代表差异物种的显著性（即为 LDA Score）。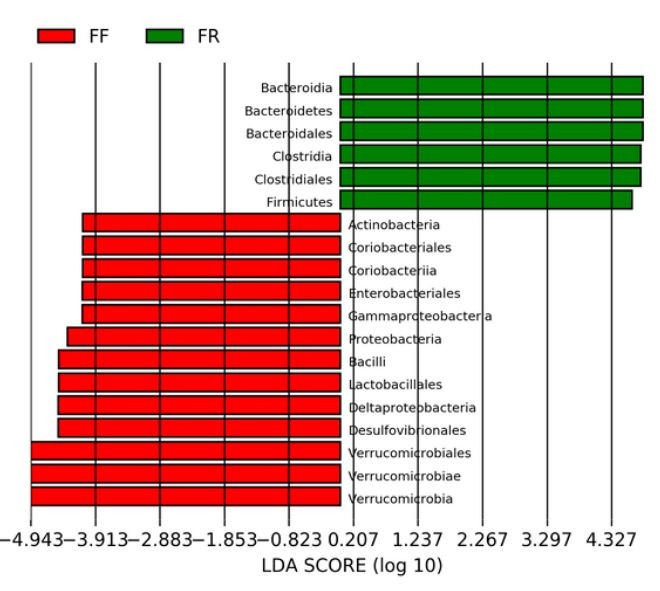
进化分支图：
在进化分支图中，由内至外辐射的圆圈代表了由界(单个圆圈)至属（或种）的分类级别(不同的分类水平下圆圈的层数不同，下图为order水平下进化图，所以有4层)。在不同分类级别上的每一个小圆圈代表该水平下的一个分类，小圆圈直径大小与相对丰度大小呈正比。着色原则：无显著差异的物种统一着色为黄色，差异物种 Biomarker跟随组进行着色，红色节点表示在红色组别中起到重要作用的微生物类群，绿色节点表示在绿色组别中起到重要作用的微生物类群，其它圈颜色意义类同。图中英文字母表示的物种名称在右侧图例中进行展示。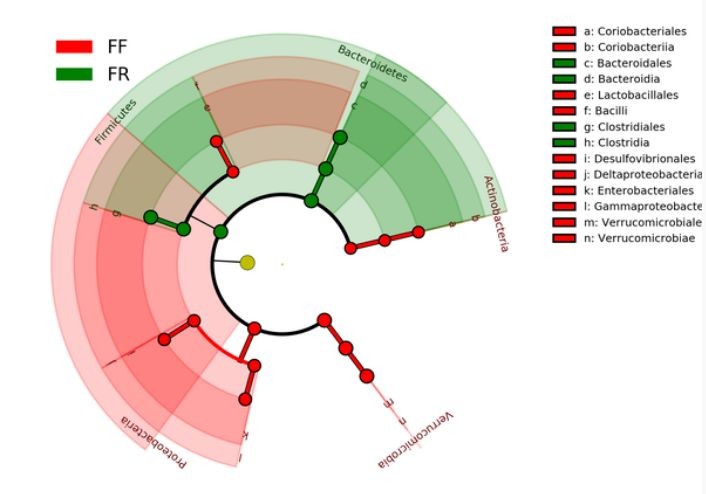
课程推荐：微生物扩增子分析课程实操 微生物16S/ITS/18S分析原理及结果解读
延伸阅读
微生物测序原理|肠道君|什么是OTU|alpha多样性|Beta多样性|GraPhlAn树状图|OTU网络图MENA
- 发表于 2018-05-17 21:52
- 阅读 ( 31025 )
- 分类：宏基因组
