cox回归PH假设检验

PH假设检验

英国统计学家D.R.Cox于1972年提出的比例风险回归模型（Proportional hazard regression model），简称Cox回归模型，有效地解决了对于生存资料进行多因素分析的问题。

但是Cox回归模型在应用时，有一个非常重要的前提条件，即比例风险（Proportional hazards）假定，简称PH假定。

PH假定的基本假设为：协变量对生存率的影响不随时间的改变而改变，即风险比值h(t)/h0(t)为固定值。而在实际进行生存分析的过程中，有些自变量对风险函数（事件发生概率）的影响会随时间的变化而变化，因此在构建Cox回归模型之前，必须对PH假定进行判定，只有PH假定得到满足时，Cox回归模型的结果才有意义。

是否符合PH假设判断

模型诊断——PH假定。PH假定可通过假设检验和残差图检验。正常情况下，Schoenfeld残差应该与时间无关，如果残差与时间有相关趋势，则违反PH假设的证据。残差图上，横轴代表时间，如果残差均匀的分布则，表示残差与时间相互独立。

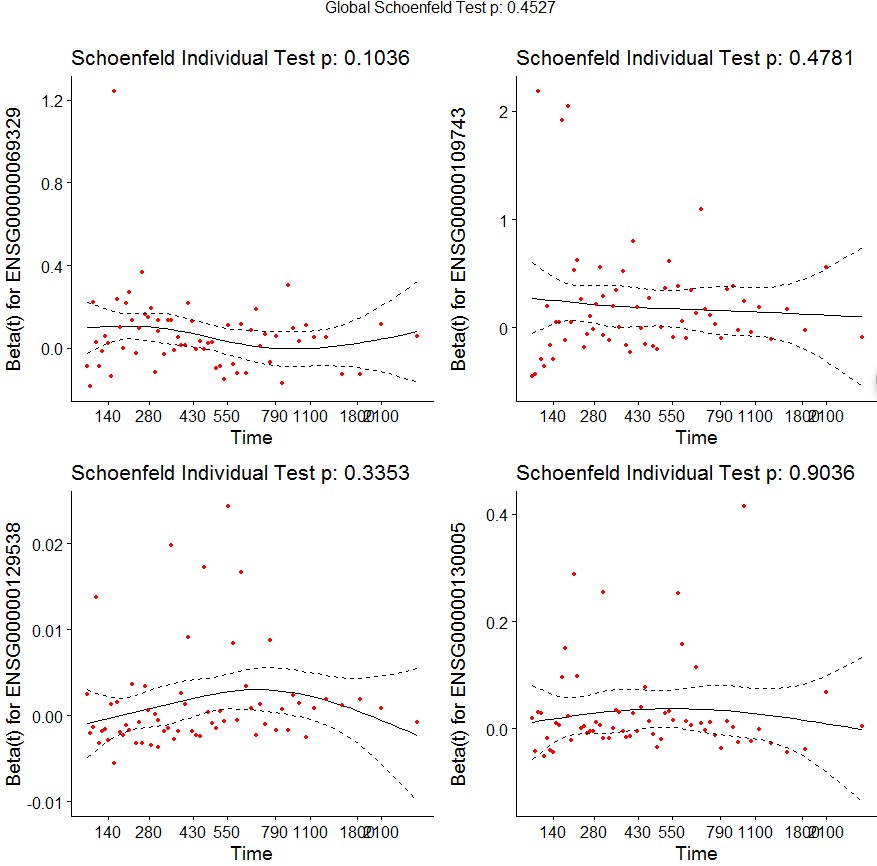
从上面的结果可以看出，三个变量的P值都大于0.05，说明每个变量均满足PH检验，而模型的整体检验P值0.1036，模型整体满足PH检验。上图中实线是拟合的样条平滑曲线，虚线表示拟合曲线上下2个单位的标准差。如果曲线偏离2个单位的标准差则表示不满足比例风险假定。从上图中可见，各协变量满足PH风险假设。

发表于 2019-12-03 15:36
阅读 ( 11183 )
分类：TCGA