Cox与KM生存分析及结果解读
生存分析：针对于慢性病(癌症)，因为其无法在短时间内判断预后，不宜采用治愈率和病死率等指标，而是需要对患者进行随访，分析一定时间后患者生存或死亡的情况，这样将事件的结果和出现这一结果所经历的时间结合起来分析的统计方法称为生存分析。
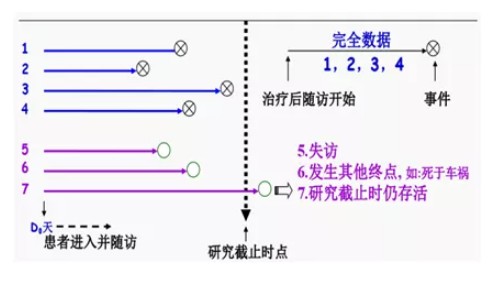
生存分析KM法与Cox法异同介绍
KM 方法即Kaplan-Meier survival estimate是一种无参数方法(non-parametric)来从观察的生存时间来估计生存概率的方法。KM生存分析模型，是单变量分析(univariable analysis)，在做单变量分析时，模型只描述了该单变量和生存之间的关系而忽略其他变量的影响。（为什么要考虑multi-variables？比如在比较两组病人拥有和不拥有某种基因型对生存率的影响，但是其中一组的患者年龄较大，所以生存率可能受到基因型 或/和 年龄的共同影响）。同时，Kaplan-Meier方法只能针对分类变量（治疗A vs 治疗B，男 vs 女），不能分析连续变量对生存造成的影响。为了解决上述两种问题，Cox比例风险回归模型（Cox proportional hazards regression model）就被提了出来。因此，Cox比例风险回归模型，可以分析连续变量对生存造成的影响，也可以多变量分析对生存的影响。
R语言中的生存分析R包介绍
R是数据分析常用的软件之一，通过各种功能强大的R包，可以简单方便的实现各种分析。在R语言中，能够进行生存分析的R包很多，survival和survminer是其中最基本的两个，survival负责分析，survimner负责可视化，二者相结合，可以轻松实现生存分析。
R语言中的KM模型分析
1. 准备生存数据
对于每个个体而言，其生存数据会出现两种情况，第一种是观测到生存时间，通常用1表示，第二种则是删失。通常用0表示。survival自带了一个测试数据lung, 内容如下所示
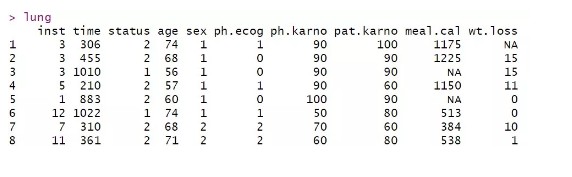
每一行代表一个样本，time表示生存时间，status表示删失情况，这里只有1和2两种取值，默认排序后的第一个level对应的值为删失，这里则为1表示删失。其他列为样本对应的性别，年龄等基本信息。
2. 进行生存分析
这里根据性别这个二分类变量，采用KM算法来估计生存曲线，代码如下(summary结果只显示部分）
> library("survival")
> library("survminer")
> kmfit<-survfit(Surv(time, status) ~ sex, data = lung)
> summary(kmfit)
Call: survfit(formula = Surv(time, status) ~ sex, data = lung)
sex=1
time n.risk n.event survival std.err lower 95% CI upper 95% CI
11 138 3 0.9783 0.0124 0.9542 1.000
12 135 1 0.9710 0.0143 0.9434 0.999
13 134 2 0.9565 0.0174 0.9231 0.991
15 132 1 0.9493 0.0187 0.9134 0.987
26 131 1 0.9420 0.0199 0.9038 0.982
30 130 1 0.9348 0.0210 0.8945 0.977
从kmfit中summary可以看到已经包含了每个时间点的生存概率，删失等信息，通过这些信息，完全可以自己写代码来画图。为了方便，我们直接采用survminer中的函数来进行可视化。
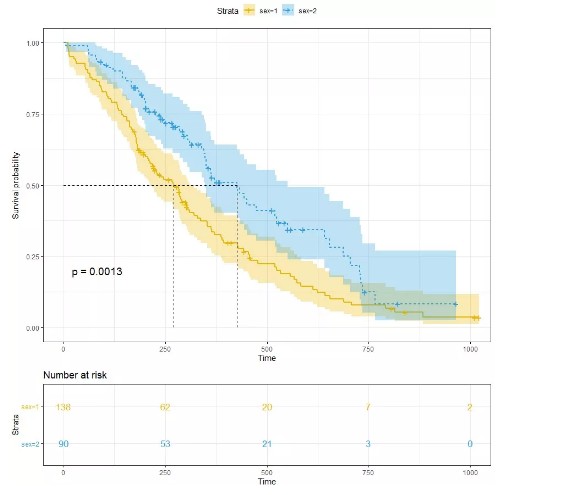
3. 分析结果的可视化
最基本的可视化方式如下
library("survminer")
ggsurvplot(kmfit,
pval = TRUE, conf.int = TRUE,
risk.table = TRUE,
risk.table.col = "strata",
linetype = "strata",
surv.median.line = "hv",
ggtheme = theme_bw(),
palette = c("#E7B800", "#2E9FDF"))
语言中的Cox模型分析
1.单变量Cox回归
library("survival")
library("survminer")
res.cox <- coxph(Surv(time, status) ~ sex, data = lung)
summary(res.cox)
res.cox <- coxph(Surv(time, status) ~ sex, data = lung)
summary(res.cox)
summary的结果：
Call:
coxph(formula = Surv(time, status) ~ sex, data = lung)
n= 228, number of events= 165
coef exp(coef) se(coef) z Pr(>|z|)
sex -0.5310 0.5880 0.1672 -3.176 0.00149 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
exp(coef) exp(-coef) lower .95 upper .95
sex 0.588 1.701 0.4237 0.816
Concordance= 0.579 (se = 0.021 )
Likelihood ratio test= 10.63 on 1 df, p=0.001
Wald test = 10.09 on 1 df, p=0.001
Score (logrank) test = 10.33 on 1 df, p=0.001
Cox回归结果可以解释如下：
统计显着性。标记为“z”的列给出了Wald统计值。它对应于每个回归系数与其标准误差的比率（z = coef / se（coef））。wald统计评估是否beta（ββ）系数在统计上显着不同于0。从上面的输出，我们可以得出结论，变量性别具有高度统计学意义的系数。
回归系数。Cox模型结果中要注意的第二个特征是回归系数（coef）的符号。一个积极的信号意味着危险（死亡风险）较高，因此对于那些变量值较高的受试者，预后更差。变量性被编码为数字向量。1：男，2：女。Cox模型的R总结给出了第二组相对于第一组，即女性与男性的风险比（HR）。性别的β系数= -0.53表明在这些数据中，女性的死亡风险（低存活率）低于男性。
危害比例。指数系数（exp（coef）= exp（-0.53）= 0.59）也称为风险比，给出协变量的效应大小。例如，女性（性别= 2）将危害降低了0.59倍，即41％。女性与预后良好相关。
风险比的置信区间。总结结果还给出了风险比（exp（coef））的95％置信区间的上限和下限，下限95％界限= 0.4237，上限95％界限= 0.816。全球统计学意义的模型。最后，输出为模型的总体显着性提供了三个替代测试的p值：可能性比率测试，Wald测试和得分logrank统计。这三种方法是渐近等价的。对于足够大的N，他们会得到相似的结果。对于小N来说，它们可能有所不同。似然比检验对于小样本量具有更好的表现，所以通常是优选的。
2.多变量Cox回归
要一次性将单变量coxph函数应用于多个协变量，请输入：
res.cox <- coxph(Surv(time, status) ~ age + sex + ph.ecog, data = lung)
summary(res.cox)
Call:
coxph(formula = Surv(time, status) ~ age + sex + ph.ecog, data = lung)
n= 227, number of events= 164
(1 observation deleted due to missingness)
coef exp(coef) se(coef) z Pr(>|z|)
age 0.011067 1.011128 0.009267 1.194 0.232416
sex -0.552612 0.575445 0.167739 -3.294 0.000986 ***
ph.ecog 0.463728 1.589991 0.113577 4.083 4.45e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
exp(coef) exp(-coef) lower .95 upper .95
age 1.0111 0.9890 0.9929 1.0297
sex 0.5754 1.7378 0.4142 0.7994
ph.ecog 1.5900 0.6289 1.2727 1.9864
Concordance= 0.637 (se = 0.025 )
Likelihood ratio test= 30.5 on 3 df, p=1e-06
Wald test = 29.93 on 3 df, p=1e-06
Score (logrank) test = 30.5 on 3 df, p=1e-06
所有3个整体测试（可能性，Wald 和 得分）的p值都是显着的，表明该模型是显着的。这些测试评估了所有的beta（ββ）为0.在上面的例子中，检验统计是完全一致的，综合零假设被完全拒绝。
在多变量Cox分析中，协变量性别和ph.ecog仍然显着（p <0.05）。然而，协变量年龄并不显着（P = 0.17，这比0.05）。
性别p值为0.000986，危险比HR = exp（coef）= 0.58，表明患者性别和死亡风险降低之间有很强的关系。协变量的风险比可以解释为对风险的倍增效应。例如，保持其他协变量不变，女性（性别= 2）将危害降低0.58倍，即42％。我们的结论是，女性与良好的预后相关。
类似地，ph.ecog的p值是4.45e-05，危险比HR = 1.59，表明ph.ecog值与死亡风险增加之间的强关系。保持其他协变量不变，ph.ecog值越高，生存率越差。
相比之下，年龄的p值现在是p = 0.23。风险比HR = exp（coef）= 1.01，95％置信区间为0.99至1.03。由于HR的置信区间为1，这些结果表明，年龄在调整了ph值和患者性别后对HR的差异的贡献较小，并且仅趋向显着性。例如，保持其他协变量不变，额外的年龄会导致每日死亡危险因素为exp（beta）= 1.01或1％，这不是一个重要的贡献。
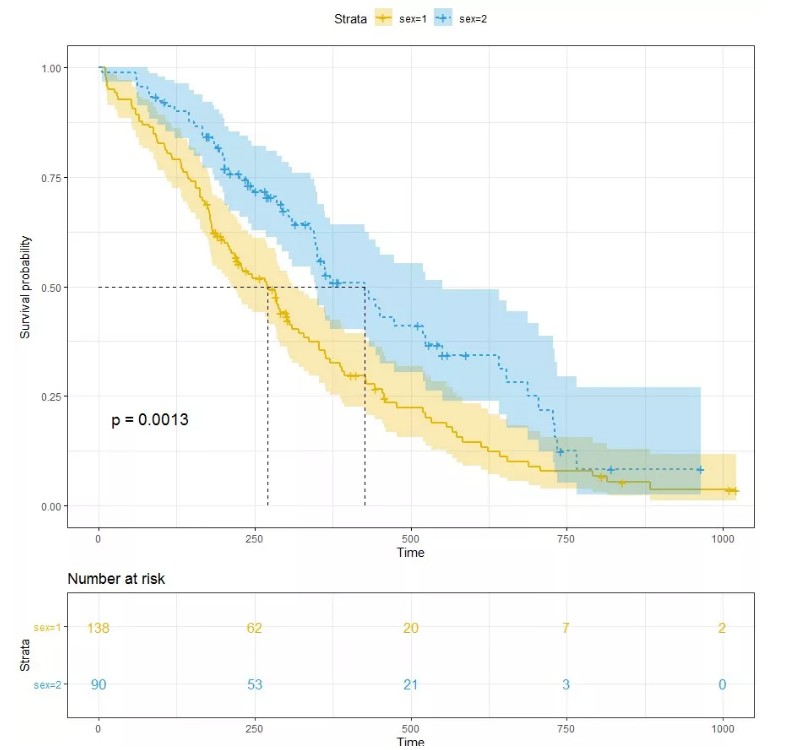
可视化估计的生存时间分布
已经将Cox模型拟合到数据中，可以在特定风险组的任何给定时间点可视化预测的存活比例。函数survfit（）估计生存比例，默认情况下为协变量的平均值。
绘制生存曲线：
kmfit<-survfit(Surv(time, status) ~ sex, data = lung)
ggsurvplot(kmfit,
pval = TRUE, conf.int = TRUE,
risk.table = TRUE,
risk.table.col = "strata",
linetype = "strata",
surv.median.line = "hv",
ggtheme = theme_bw(),
palette = c("#E7B800", "#2E9FDF"))
延伸阅读
TCGA数据下载—TCGAbiolinks包参数详解
更多生物信息课程：
1. 文章越来越难发？是你没发现新思路，基因家族分析发2-4分文章简单快速，学习链接：基因家族分析实操课程、基因家族文献思路解读
2. 转录组数据理解不深入？图表看不懂？点击链接学习深入解读数据结果文件，学习链接：转录组（有参）结果解读；转录组（无参）结果解读
3. 转录组数据深入挖掘技能-WGCNA，提升你的文章档次，学习链接：WGCNA-加权基因共表达网络分析
4. 转录组数据怎么挖掘？学习链接：转录组标准分析后的数据挖掘、转录组文献解读
5. 微生物16S/ITS/18S分析原理及结果解读、OTU网络图绘制、cytoscape与网络图绘制课程
6. 生物信息入门到精通必修基础课：linux系统使用、biolinux搭建生物信息分析环境、linux命令处理生物大数据、perl入门到精通、perl语言高级、R语言画图、R语言快速入门与提高、python语言入门到精通
7. 医学相关数据挖掘课程，不用做实验也能发文章：TCGA-差异基因分析、GEO芯片数据挖掘、 GEO芯片数据不同平台标准化 、GSEA富集分析课程、TCGA临床数据生存分析、TCGA-转录因子分析、TCGA-ceRNA调控网络分析
8.其他，二代测序转录组数据自主分析、NCBI数据上传、二代fastq测序数据解读、
9.全部课程可点击：组学大讲堂视频课程
- 发表于 2019-12-11 18:02
- 阅读 ( 36443 )
- 分类：TCGA
