群落分析的冗余分析(RDA)概述
扩增子分析视频课程推荐:https://bdtcd.xetslk.com/s/qZRiF
约束排序之冗余分析(RDA)概述
前篇先后简介了主成分分析(PCA)、对应分析(CA)、主坐标分析(PCoA)以及非度量多维尺度分析(NMDS)。这些排序方法均属于非约束排序,只涉及一个数据矩阵,并在低维空间中尽可能呈现原始的数据结构。非约束排序方法中不存在解释变量(对于物种多度数据而言,解释变量通常指代环境因素),尽管可以通过相关性或多元回归的方式被动添加至排序空间中。与此相比,约束排序则可以从排序开始直接加入解释变量进行运算,它涉及两个数据矩阵,响应变量矩阵以及解释变量矩阵。本篇继续以群落分析为例,对约束排序方法之一的冗余排序(RDA)作个简述。
RDA的基本方法描述
冗余分析(RDA)和基于转化的冗余分析(tb-RDA)
Rao(1964)首次提出冗余分析(Redundancy analysis,RDA),从概念上讲,RDA是响应变量矩阵与解释变量矩阵之间多元多重线性回归的拟合值矩阵的PCA分析,也是多响应变量(multi-response)回归分析的拓展。在群落分析中常使用RDA,将物种多度的变化分解为与环境变量相关的变差(variation;或称方差,variance,因为RDA中变差=方差;由约束/典范轴承载),用以探索群落物种组成受环境变量约束的关系。
包含很多零值的物种多度数据在执行多元回归或其它基于欧式距离的分析方法之前必须被转化,Legendre和Gallagher(2001)提出的基于转化的RDA(Transformation-based redundancy analysis,tb-RDA)用于解决这个问题。tb-RDA在分析前首先对原始数据做一定的转化(例如Hellinger预转化包含很多零值的群落物种数据),并使用转化后的数据执行RDA。即除了第一步增添了数据转化外,其余过程均和常规的RDA相同,只是在原始数据本身做了改动,RDA算法本质未变。
RDA算法可以简要总结如下(详细过程可参阅Legendre和Legendre(1998)“Numerical Ecology”,579-584页的内容)。其中矩阵Y是中心化的响应变量矩阵,X矩阵是中心化(或标准化)的解释变量矩阵。RDA中通常使用标准化后的解释变量,因为在很多情况下解释变量具有不同的量纲,解释变量标准化的意义在于使典范系数的绝对值(即模型的回归系数)能够度量解释变量对约束轴的贡献,解释变量的标准化不会改变回归的拟合值和约束排序的结果。在群落分析中,响应变量矩阵一般即为物种多度数据,解释变量矩阵即为环境变量数据。
(1)先将矩阵Y中的每个响应变量分别与矩阵X中的所有解释变量进行多元回归,通过回归模型获得每个响应变量的拟合值(fitted values,即在回归线上对应的值)以及残差(residuals,响应变量的观测值和拟合值之间的差值),最终得到包含所有响应变量拟合值及残差的拟合值矩阵Ŷ以及残差矩阵Yres)。
(2)对拟合值矩阵Ŷ运行PCA,得到典范特征向量(eigenvectors)矩阵U。使用矩阵U计算两套样方排序得分(坐标):一套使用中心化的原始数据矩阵Y获得在原始变量Y空间内的样方排序坐标(即计算YU,所获得的坐标称为“样方得分”,即物种得分的加权和);另一套使用拟合值矩阵Ŷ获得在解释变量X空间内的样方排序坐标(即计算ŶU,所获得的坐标称为“样方约束”,即约束变量的线性组合)。
(3)一般来讲,RDA过程执行到上步就算完成了。但一般情况下我们会同时对残差矩阵Yres运行PCA,获得残差非约束排序。非约束轴即代表了解释变量未能对响应变量作出解释的部分,严格地来说不属于RDA的范畴,但能够帮助我们获取更多信息。
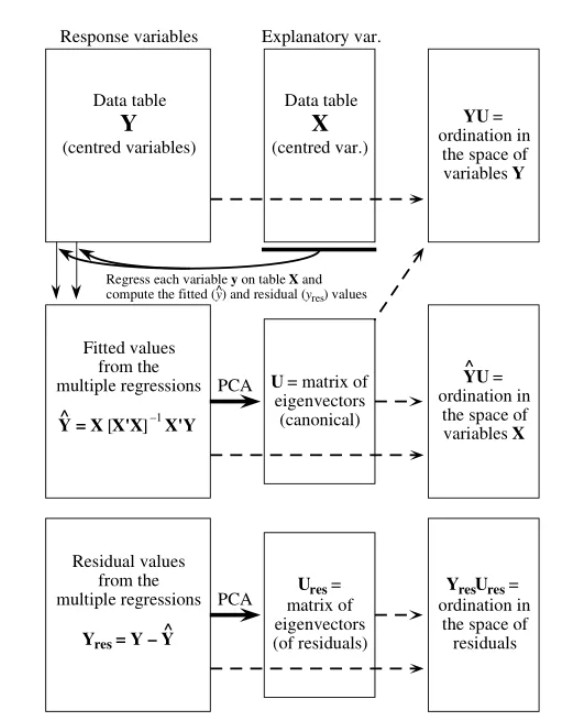
Zelený博士使用仅包含一个解释变量(环境变量)的数据形象化地展示了RDA过程(原文:https://www.davidzeleny.net/anadat-r/doku.php/en:rda_cca)。
(1)执行物种spe1与环境变量env1的线性回归(由于此处示例中仅存在一个环境解释变量,故此回归为一元线性回归;当存在多解释变量时,即为多元线性回归),将回归模型拟合的物种丰度值存储在拟合值矩阵,物种丰度的残差存储在残差矩阵。见下图1中所示的过程。
(2)如此对物种组成矩阵中的所有物种重复相同的操作,最终获得包含所有物种丰度拟合值及残差的两个矩阵。见下图2中所示的两个矩阵。(1)(2)过程即形象化地展示了RDA中的回归细节部分。
(3)回归过程执行完毕后,使用PCA,在拟合值矩阵中提取约束的排序轴,并在残差值矩阵中提取非约束的轴。见下图2中所示的过程,在该示例中,由于仅有一个解释变量(环境变量env1),因此仅得到一个约束的排序轴(排序图中的垂直轴是第一个非约束轴)。

RDA排序结果产生的约束轴的数量为min[p, m, n - 1];如果同时获得非约束排序结果(即PCA),则非约束轴数量为min[p, n - 1]。其中,p为响应变量数量;m为定量解释变量数量以及定性解释变量(因子变量)的因子水平的自由度(即该变量因子水平数减1);n为排序对象数量。
偏冗余分析(偏RDA)
偏冗余分析(Partial canonical ordination,偏RDA)相当于多元偏线性回归分析(Davies和Tso,1982),在实际应用中同样广泛。
与偏线性回归相似,解释变量被分为两组:X和W,其中X表示模型中将被考虑的解释变量,W表示对响应变量Y的影响被控制的协变量。若变量矩阵W对响应变量Y的影响已知,在这种情况下,我们常期望在控制W对Y的影响的前提下,将关注点集中在另一组变量矩阵X对响应变量Y的影响上。例如,可以以气候变量X作为解释变量,土壤因子变量W作为协变量,对群落物种数据进行RDA分析。这样分析的目的是在控制土壤因子影响后,展示单独能够被气候变量线性模型解释的物种格局。
在解释变量的前向选择过程中,偏RDA应用广泛。
基于距离的冗余分析(db-RDA)
尽管tb-RDA的应用拓展了RDA的适用范围,但无论常规的RDA或tb-RDA,样方或物种的降维过程实质上均以欧氏距离为基础。有时我们可能期望关注非欧式距离样方或物种关系的RDA。
Legendre和Anderson(1999)提出的基于距离的冗余分析(Distance-based redundancy analysis,db-RDA)用于解决这个问题,并且证明RDA能够以方差分析方式分析由用于选择的任何距离矩阵。db-RDA将主坐标分析(PCoA)计算的样方得分矩阵应用在RDA中,其好处是可以基于任意一种距离测度(例如Bray-curtis距离等,而不再仅仅局限于欧氏距离)进行RDA排序,因此db-RDA在生态学统计分析中被广泛使用。当然,若是我们直接计算样方群落间的欧式距离矩阵并将其输入至db-RDA中计算时,也将会得到和常规的RDA一致的结果。
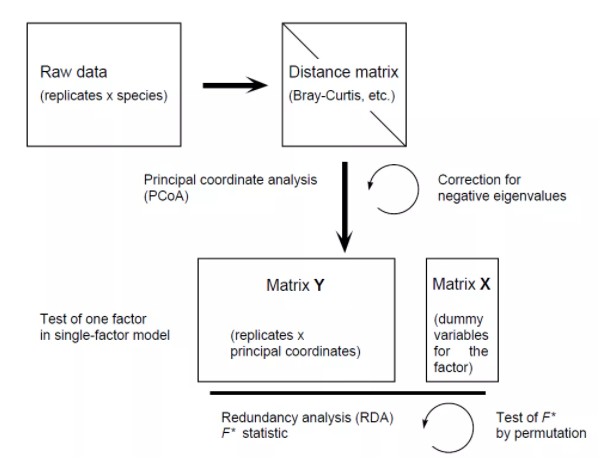
db-RDA首先基于物种多度数据(根据实际需求,选择使用原始物种数据或经过某种转化后的物种数据)计算相异矩阵(如Bray-curtis距离矩阵),作为PCoA的输入,之后将所有PCoA排序轴上的样方得分矩阵用于执行RDA,而不再使用原始的物种数据以及解释变量(环境因子数据)直接作为RDA的输入。由于在PCoA中可能会产生负特征值,必要时需要引入一些有效的校正方法。
尽管物种信息在相异矩阵的计算过程中丢失,但主坐标矩阵依然可以视为表征数据总变差的距离矩阵,因此db-RDA结果反映了解释变量对从整个响应数据中得出的样方相似性(相异矩阵)的影响。若期望补充物种得分,方法与PCoA中过程一致,物种得分可以通过与它们所在样方得分的多度加权平均与PCoA轴建立关联而投影到最终的排序图中,用以表明响应变量(即物种信息)对PCoA排序的贡献程度。
非线性关系的冗余分析
RDA是通过多元线性回归分析后获得的拟合值矩阵的PCA分析,因此,很多用于多元回归的技术都可以在RDA中使用。上面所有的RDA模型都仅使用一阶的解释变量。然而,物种分布对环境梯度通常是单峰响应(如下图所示),即物种通常有最适合的生态区域。因此,对于这种情况一阶线性模型可能不太适用。
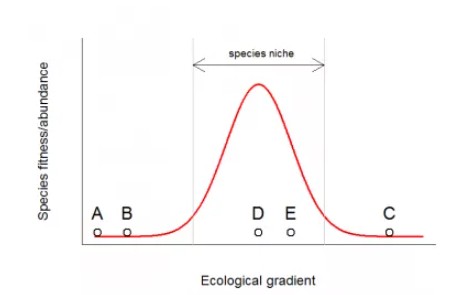
图注:单一物种沿环境梯度的单峰响应曲线。D为该物种的最适环境梯度,E为较适环境,A、B、C则为位于该物种生态位外(对于该物种来讲此时环境很极端,难以生存或增长)。
绘制所有响应变量与单个解释变量之间的散点图检验非线性关系非常繁琐,识别和拟合单峰响应最简单模式是在一阶函数基础上加入二阶解释变量(即二次项)并运行变量的前向选择,以保留某些一阶或二阶变量。然而,含有二阶解释变量的RDA结果很难解读,所以只有充分理由认为是非线性关系时才能使用非线性的RDA。三阶的解释变量也可以用于拟合单峰响应关系,但需要高偏态分布的响应变量。原始的多项式通常高度相关,因此建议使用正交的多项式。
需注意,所有的非线性RDA仅使用非转化的响应变量。
RDA结果解读
从上述解释计算RDA的步骤中即可看出,RDA的排序轴实际上是解释变量的线性组合(即线性模型拟合值的排序)。换句话说,RDA的目的是寻找能最大程度解释响应变量矩阵变差的一些列的解释变量的线性组合,因此RDA是被解释变量约束的排序。约束排序与非约束排序的区别很明显:约束排序过程中解释变量矩阵控制排序轴的权重(特征根)、正交性和方向。在RDA中,排序轴解释或模拟(从统计意义上讲)依赖矩阵(响应变量)的变差,并可以检验响应变量矩阵Y与解释变量矩阵X的线性相关显著性;非约束排序PCA分析则不存在这种情况。尽管在非约束模型中,可以通过在排序后被动地加入解释变量以达到解释排序轴的目的(详见前文),但此举与约束排序相比具有本质区别。
在群落分析中,对于非约束排序模型(如PCA),我们感兴趣的信息主要是排序图中样方和物种变量得分的相对位置、部分排序轴的相对重要性(根据特征值判断)以及排序轴的生态解释等;而对于约束排序模型(如RDA),我们通常更关注环境变量对物种组成的影响(即环境变量所能解释的变差,以及解释程度的显著性)、哪些环境变量对于群落结构的解释更为重要(变量选择)以及获知各变量或变量集解释的变差(变差分解)等。这些相关的延伸(也很重要)内容不在本文中介绍,若有需要可点击对应链接阅读。
变差(方差)解释程度
通常情况下我们在执行RDA时(如使用R语言vegan包的rda()函数运行RDA),能够同时获得约束轴(即解释变量能够解释的部分,以约束轴呈现)和非约束轴(即解释变量未能解释的部分,多元回归的残差部分,该部分以非约束轴呈现)两部分信息,原始响应变量矩阵的总变差为约束轴解释变差和非约束轴解释变差的加和。
同前述非约束排序PCA,在RDA概念中,变差=方差。
RDA的约束轴
约束模型解释变差反映了响应变量变化量的多少与解释变量有关,如果用比例表示,其值相当于多元回归的R2,这个解释比例值也称作双多元冗余统计(Bimultivariate redundancy statistic)。然而,类似于多元回归的未校正R2,RDA的R2也是有偏差的,需要进行校正。
同时,并非每一个约束轴都是合理有效的,还需依据置换的原理检验各约束轴的显著性,对约束轴进行取舍(详见前文)。因此,与非约束模型PCA等的非约束轴等不同,RDA约束轴的评判方法比较严格,若约束轴未通过检验,则不应被选择。(PCA只是探索性分析方法,非约束轴的选择并无严格的标准;RDA已经涉及了统计检验的过程,显著性通过p值衡量)
RDA的非约束轴
如上所述,也就是约束轴未能解释的,多元回归的残差部分,额外以非约束PCA轴作为呈现。对RDA进行解读时,最好同时结合约束轴和非约束轴中的信息,尽管非约束部分严格来讲不属于RDA范畴,但很多情形中仍具参考价值。
群落分析中,常通过RDA描述环境变量(解释变量)解释样方物种组成(响应变量)的差异。如果约束轴解释的变差大于非约束轴解释的变差,表明响应数据的大部分变化量均可通过解释变量作出解释,群落物种组成分布真实地由给定环境因子所影响(对于RDA结果,即二者呈现出较好的线性梯度);如果约束轴解释变差低于非约束轴解释变差,或者约束轴解释变差仅占总变差的较小比例,此时应谨慎对待,因为模型并未显示出给定环境因子能够对群落物种的组成作出有效的解释。
约束模型解释量偏低的原因可能是还有重要的解释变量尚未考虑,或是解释变量之间存在交互作用,或者归因于实际群落中物种和环境的复杂关系通常很难仅通过简单的模型有效描述出等(例如常规的RDA基于一阶线性模型,但物种和环境的关系多数情况下并非一阶线性关系,这种情况下,物种分布可能并非不受这些环境因子的约束,仅仅归因于简单的一阶线性模型无法有效描述其关系)。
排序轴特征值和解释率
RDA中每一个约束轴的特征值(eigenvalue)与特征值总和(约束轴和非约束轴特征值总和)的比例即为该轴的解释率。所有约束轴解释率总和即R2。因此,对于合理的RDA模型来讲,选定轴(通常选取特征值最高的前2-3轴用来观测)的解释量不能太低。
少数情况下,残差之间的排序或相关性(非约束轴)可能比具有良好特征的约束轴更具生物学意义。如上所述,对于RDA的残差,即额外以PCA轴的形式呈现。如果有必要,通过观测非约束空间中的样方和物种的相对位置可以帮助解读这些残差的特征。
RDA排序图
维度选择
对于排序对象、解释变量以及响应变量的相互关系,最终通过排序图直观呈现。一般而言,我们仅选择前2-3个特征值较高(且显著)的约束轴用于观测(并尝试对其做出解释),并表示为二维/三维散点图的样式,少数情况下也会根据实际情况选择特定的排序轴(例如第二轴的趋势不明显,第三轴反而明显,因此跳过了第二轴,使用二维点图对第一、三轴可视化并做出解释;有时也会选择使用两个二维点图,分别展示并解释第一、二和三、四轴等)。有一点需要切记,就是不要试图解释太多的轴,太多的生态维度反而意义不大,正如McCune和Grace(2002)所说:“Very few ecologists have dared to venture into the uncertain waters of four or more dimensions”。
排序图表示
以R语言vegan包分析群落数据为例,排序对象(样方)、响应变量(物种)以及解释变量(环境变量)在各个约束轴中的排序结果分别报告为样方得分(site scores)、物种得分(species scores)以及解释变量得分(explanatory variable scores),投影到排序图中即表示为坐标轴上对应位置处的坐标。根据是否展示物种向量,排序图可分为双序图(仅展示样方和环境变量二者关系)和三序图(展示样方、物种及环境变量三者关系)。
RDA排序图中,样方直接在对应坐标处绘制为点。物种变量则呈现为向量,由原点(0,0)起始,指向物种得分的对应坐标处,向量的方向表示了该物种丰度增加的方向。解释变量得分(explanatory variable scores)同样以向量的形式表示在RDA排序图中,环境向量的长度表示样方物种的分布与该环境因子相关性的大小;向量与约束轴夹角的大小表示环境因子与约束轴相关性的大小,夹角小说明关系密切,若正交则不相关。
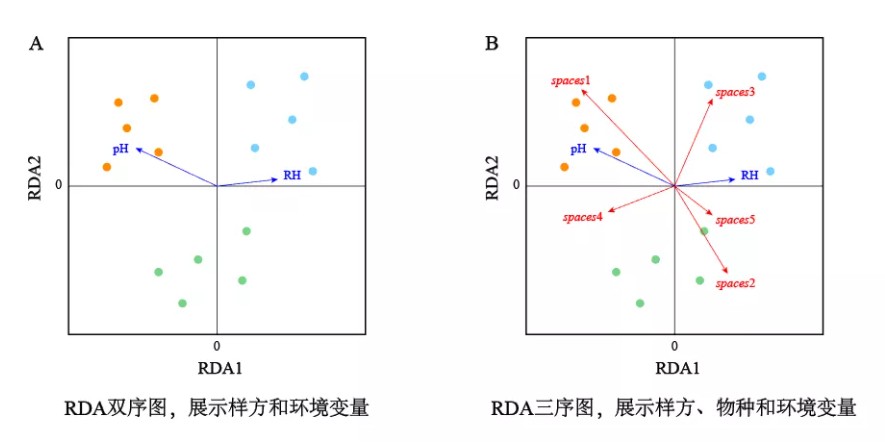
图注:二维散点图展示某RDA结果的前两个约束轴。其中A图为双序图,展示样方和环境变量;B图为三序图,展示样方、物种和环境变量。
PCA中有I、II型标尺的选择,RDA中也是如此。
无论RDA双序图或三序图,均需要同时展示对象和变量,但没有同时可视化对象和变量的最优化方法。通常根据关注侧重点的不同,考虑使用不同的标度(或称尺度、标尺)展示排序图,以重点反映关键的信息。得分集作为RDA输出的典型特征,将根据使用的标度而变化。一般有两种标尺模式,不同模式的排序图有不同的解读方式。如果对排序样方之间的距离更感兴趣,或者大多数解释变量为因子类型,则考虑I型标尺;如果对变量之间的相关关系更感兴趣,则考虑II型标尺。
在两种标尺的RDA排序图内,对于双序图,由于未展示物种信息故无需考虑样方和物种关系的解读方式;对于三序图,样方和物种箭头的解读同PCA,将样方对象点垂直投影到物种变量箭头上位置表示该物种在该样方内数值在所有样方内的排序位置。但是,解释变量的箭头或因子变量的形心的解读另有规则。
以下是对RDA I型标尺和II型标尺的简要描述(详细过程可参阅Legendre和Legendre(1998)“Numerical Ecology”,585-587页的内容)。
RDA的I型标尺
I型标尺关注的是对象之间的关系。矩阵U的特征向量(代表了约束轴中的响应变量得分,参见开头“RDA算法简述”,下述X、Y、Ŷ等同述),被标准化为单位长度。X空间内的样方得分由公式Z=ŶU获得,这些向量具有相同的方差λk。Y空间内的样方得分由公式F=YU获得,这些向量的方差通常显著高于λk,因为Y同时涵括了拟合值和残差值因此其总方差高于Ŷ(仅为拟合值)的方差。通过双序图表示矩阵Z和U,或F和U时,特征向量与样方得分矩阵的结果较好地还原了原始矩阵:ZU’=Ŷ或FU’=Y。对于定量解释变量x与样方得分拟合值的相关性,乘以(λk/Y的总方差)1/2后在各排序轴中呈现,其中λk为约束轴k的特征值。在这种标尺中,各约束轴中的样方得分具有不同的方差。
I型标尺的RDA排序图主要展示如下信息:
(1)样方点垂直投影到响应变量或定量解释变量的箭头或延长线上,投影点近似于该样方内该响应变量或解释变量的数值沿着变量的位置;
(2)响应变量与解释变量箭头之间的夹角反映了它们之间的相关性(但响应变量之间的夹角无此含义);
(3)定性解释变量的形心与响应变量(物种)箭头之间的解读如同样方点与响应变量之间的解读(因为定性解释变量的形心也是一组样方的形心);
(4)定性解释变量的形心之间或形心与样方点之间的距离近似他们之间的欧式距离。
RDA的II型标尺
II型标尺中,每个特征向量被标准化为特征根的平方根,关注的是变量之间的关系。
通过UɅ1/2转化,将矩阵U的特征向量(代表了约束轴中的响应变量得分,参见开头“RDA算法简述”,下述X、Y、Ŷ等同述)标准化为(λk)1/2。X空间内的样方得分通过Z=ŶU获得后,再经ZɅ-1/2转化缩放为单位方差。同样地,Y空间内的样方得分通过F=YU获得后,再经FɅ-1/2转化缩放,并且所得向量的方差通常显著高于由X所得向量的方差,原因同上述“I型标尺”中的描述。通过双序图表示矩阵Z和U,或F和U时,特征向量与样方得分矩阵的结果较好地还原了原始矩阵:ZU’=Ŷ或FU’=Y。定量解释变量x与样方得分拟合值的相关性直接呈现在各排序轴中。
II型标尺的RDA排序图主要展示如下信息:
(1)将样方点垂直投影到响应变量或定量解释变量的箭头或延长线上,投影点位置近似于该响应变量或解释变量在该样方内的数值;
(2)响应变量与解释变量箭头之间的夹角反映它们之间的相关性,响应变量之间和解释变量之间也同样解读;
(3)定性解释变量的形心与响应变量箭头之间的解读如同样方点与响应变量之间的解读,可以通过投影点判断;
(4)定性解释变量的形心之间或形心与样方之间的距离不再近似欧式距离。
看完描述是不是有点懵?接下来通过两个图来简要说明下对RDA排序图的解读吧。
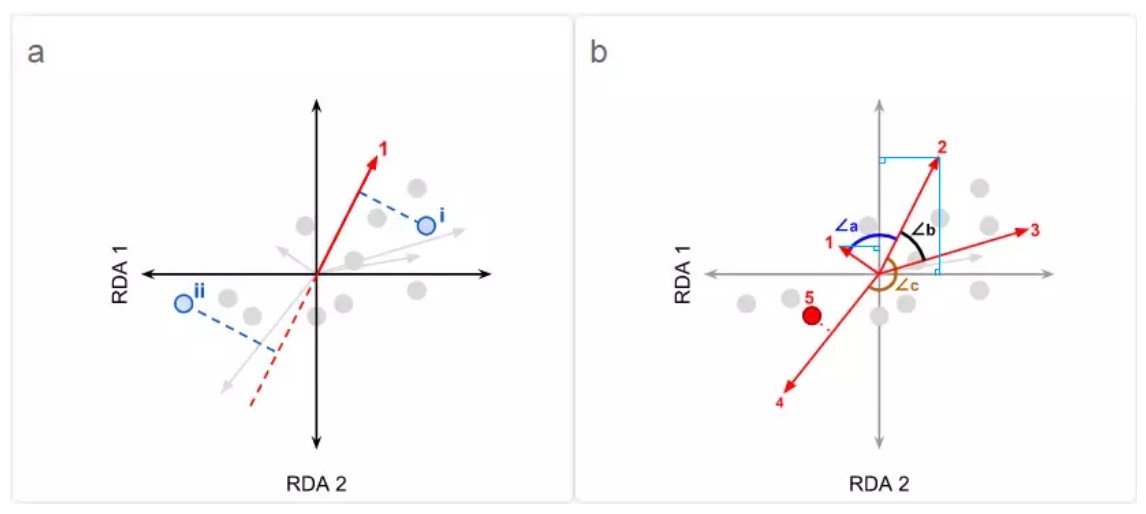
(1)a图,存在排序样方(样本)I和II,解释变量(环境变量)1,探究I或II与1的关系时,将I或II垂直投影在1的向量(箭头)上,根据交叉点的位置判断变量1在I或II中的值。交叉点越靠近该变量向量的正方向,则表明所对应的样方中,该变量的数值越大。例如,假设变量1为土壤碳含量,样方I投影在1的正方向,样方II投影在1的负方向上(图中红色虚线反向延长线部分),两个交叉点相比较,I与1的交叉点更位于1延伸方向,因此可知I中的土壤碳含量要比II中的土壤碳含量要高。
若1为响应变量(物种变量),观察方法同样适用。例如变量1为物种species1,同样据此可判断物种species1在I中的丰度高于在II中的丰度。
注:无论I型标尺或II型标尺,均可据此判断变量在样方中的相对数值大小。
(2)b图,根据向量(箭头)夹角判断变量间的相关性。∠a接近90°,即接近正交,表明变量1和2之间的相关性很小,二者相互之间几乎不存在影响。∠b小于90°,夹角为锐角,表明变量2和3之间存在正相关;锐角角度越小,则正相关性越大。∠c大于90°,夹角为钝角,表明变量3和4之间存在负相关;钝角角度越大,则负相关性越大。
注:对于I型标尺,仅可据此观测解释变量与响应变量间的相关性;对于II型标尺,既可以据此观测解释变量与响应变量间的相关性,也可以观测解释变量之间、或响应变量之间的相关性。
(3)对于因子类型的解释变量5(定性变量,非数值型变量),在图中以点表示而非以向量表示,探究变量5与其它变量间的相关性时需要根据投影判断。例如,变量5垂直投影在变量4的正方向,表明与变量4存在正相关;投影在变量2的负方向,表明与变量2存在负相关;相关性的大小,可以通过垂线交叉点与原点(0,0)的距离来表示。
注:对于I型标尺,仅能据此观测定性解释变量与响应变量间的相关性;对于II型标尺,既可以据此观测定性解释变量与响应变量间的相关性,也可以观测其与定量解释变量之间的相关性。
(4)若为I型标尺,还可根据图中样方点之间的距离判断样方群落之间的相似性。两个样方距离越近,则群落相似性越大;反之越低。
(5)此外,还可通过比较解释变量(环境变量)向量在约束轴上投影的相对长度,判断环境变量对群落特征的贡献度。例如在图b中,将变量2和变量1均投影至RDA2轴,此时变量2的投影长度相对更长,表明变量2比变量1对RDA2轴形成的贡献更大。
解释变量向量与约束轴夹角的大小同样具有意义,表示解释变量与约束轴相关性的大小,夹角小说明关系密切,若正交则不相关。例如在图b中,变量2的向量与RDA2轴的夹角比与RDA1轴的夹角更小,表明变量2与RDA2的关联程度比与RDA1的关联程度要高,即相较之下变量2更贡献于RDA2轴。
注:无论I型标尺或II型标尺,均可据此判断。
坐标位置的特殊调整
此外,在绘制排序图时,通常会考虑将排序对象或变量的得分(即坐标)乘以一个常量,即对排序图中的点或向量坐标同比例放大或缩小一定的数值后展示,以产生易于解读的生态排序结果(可参见Legendre和Legendre,1998,404页)。这种做法可能与严格的数学定义相违背,但是对于解答生物学问题通常是没有影响的。
也可参考前述博文的末尾所述。
其它内容
本篇关于RDA的基础部分,大致就先介绍这些吧,对于初步理解绝对够用了。
RDA作为多元统计分析中的常见方法,其使用范围广泛,因此目前可用于运行RDA的软件也有很多可供选择。例如,生态学统计分析的常用R包vegan中,提供了关于RDA模型计算、I型或II型标尺选择、R2校正、置换检验、变量选择、变差分解等一系列的方法,因此下一篇将简介R包vegan的RDA分析。
扩增子分析视频课程推荐:https://bdtcd.xetslk.com/s/qZRiF
参考资料
DanielBorcard, FranoisGillet, PierreLegendre, et al. 数量生态学:R语言的应用(赖江山 译). 高等教育出版社, 2014.
David Zelený博士:https://www.davidzeleny.net/anadat-r/doku.php/en:rda_cca_examples
Davies P T, Tso K S. Procedures for Reduced-Rank Regression. Journal of the Royal Statistical Society. Series C (Applied Statistics), 1982, 31(3):244-255.
GUSTA ME Blog:https://mb3is.megx.net/gustame/constrained-analyses/rda
Legendre P, Anderson M J . Distance-Based Redundancy Analysis: Testing Multispecies Responses in Multifactorial Ecological Experiments. Ecological Monographs, 1999, 69(1):1-24.
Legendre P, Gallagher E D . Ecologically Meaningful Transformations for Ordination of Species Data. Oecologia, 2001, 129(2):271-280.
Legendre P, Legendre L. Numerical Ecology. Second English edition. Developments in Environmental Modelling, 1998, 20, Elsevier
Mccune B P, Grace J B. Analysis of Ecological Communities. Journal of Experimental Marine Biology and Ecology, 2002, 289(2).
Rao C R. The use and interpretation of principal component analysis in applied research. Sankhya, A, 1964, 26(4):329-358.
更多生物信息课程:
1. 文章越来越难发?是你没发现新思路,基因家族分析发2-4分文章简单快速,学习链接:基因家族分析实操课程、基因家族文献思路解读
2. 转录组数据理解不深入?图表看不懂?点击链接学习深入解读数据结果文件,学习链接:转录组(有参)结果解读;转录组(无参)结果解读
3. 转录组数据深入挖掘技能-WGCNA,提升你的文章档次,学习链接:WGCNA-加权基因共表达网络分析
4. 转录组数据怎么挖掘?学习链接:转录组标准分析后的数据挖掘、转录组文献解读
- 发表于 2020-11-02 15:57
- 阅读 ( 46403 )
- 分类:宏基因组
你可能感兴趣的文章
- 典型相关性分析CCA与冗余分析RDA 9933 浏览
- RDA CCA 分析 15082 浏览
- RDA CCA 分析Hellinger转化问题 11504 浏览
- 排序分析PCA、PCoA、CA、NMDS、RDA、CCA等区别与联系 41918 浏览
