关于物种组成数据Hellinger的转化

一般而言，对于物种组成数据较少使用PCA这种线性模型去做，PCoA或NMDS等是比较推荐的。

如果仍要使用PCA的话，事实上，并不是说物种多度数据一定要作转化才行。如果物种多度数据比较均匀，且含有很少的0值（这是最关键的，避开了欧几里得距离对“双零”敏感这一问题），则不转化也是可以的。

比方说示例数据“phylum_table.txt”，由于是门水平（一个很大的类别）的类群统计，本身0值较少，其实也可以不执行Hellinger转化的。尽管如此，可能高丰度和低丰度种群的丰度差别还是非常大，数据并不“均匀”，此时可以通过在运行rda()时，通过“scale=TRUE”消除高丰度物种与稀有物种在重要性方面的差异，降低欧几里得距离对高数值的敏感性。

但如果0值过多，执行PCA时还是推荐Hellinger转化，我们换个数据说明下吧。

网盘文件“otu_table.txt”是OTU水平的物种丰度表，其中含有非常多的0值，然后我们比较下Hellinger转化前后的PCA差异。

#对比物种数据 Hellinger 转化前后的差异
otu <- read.delim('otu_table.txt', sep = '\t', row.names = 1, stringsAsFactors = FALSE, check.names = FALSE)
otu_hel <- decostand(otu, method = 'hellinger')
 
pca_sp1 <- rda(otu, scale = FALSE)      #使用 Hellinger 转化前的数据
pca_sp2 <- rda(otu_hel, scale = FALSE)        #使用 Hellinger 转化后的数据
pca_sp3 <- rda(otu, scale = TRUE)        #使用 Hellinger 转化前的数据，但执行标准化
 
#特征值提取
pca_exp1 <- pca_sp1$CA$eig / sum(pca_sp1$CA$eig)
pc1_sp1 <- paste('PC1:', round(pca_exp1[1]*100, 2), '%')
pc2_sp1 <- paste('PC2:',round(pca_exp1[2]*100, 2), '%')
 
pca_exp2 <- pca_sp2$CA$eig / sum(pca_sp2$CA$eig)
pc1_sp2 <- paste('PC1:', round(pca_exp2[1]*100, 2), '%')
pc2_sp2 <- paste('PC2:',round(pca_exp2[2]*100, 2), '%')
 
pca_exp3 <- pca_sp3$CA$eig / sum(pca_sp3$CA$eig)
pc1_sp3 <- paste('PC1:', round(pca_exp3[1]*100, 2), '%')
pc2_sp3 <- paste('PC2:',round(pca_exp3[2]*100, 2), '%')
 
#I 型标尺
par(mfrow = c(2, 2))
#ordiplot(pca_sp1, scaling = 1, display = 'site', type = 'text')
#ordiplot(pca_sp2, scaling = 1, display = 'site', type = 'text')
#ordiplot(pca_sp3, scaling = 1, display = 'site', type = 'text')
ordiplot(pca_sp1, dis = 'site', type = 'n', choices = c(1, 2), scaling = 1, main = 'Hellinger 前，不标准化', xlab = pc1_sp1, ylab = pc2_sp1)
points(pca_sp1, dis = 'site', choices = c(1, 2), scaling = 1, pch = 21, bg = c(rep('red', 12), rep('orange', 12), rep('green3', 12)), col = NA, cex = 1.2)
ordiplot(pca_sp2, dis = 'site', type = 'n', choices = c(1, 2), scaling = 1, main = 'Hellinger 后，不标准化', xlab = pc1_sp2, ylab = pc2_sp2)
points(pca_sp2, dis = 'site', choices = c(1, 2), scaling = 1, pch = 21, bg = c(rep('red', 12), rep('orange', 12), rep('green3', 12)), col = NA, cex = 1.2)
ordiplot(pca_sp3, dis = 'site', type = 'n', choices = c(1, 2), scaling = 1, main = 'Hellinger 前，标准化', xlab = pc1_sp3, ylab = pc2_sp3)
points(pca_sp3, dis = 'site', choices = c(1, 2), scaling = 1, pch = 21, bg = c(rep('red', 12), rep('orange', 12), rep('green3', 12)), col = NA, cex = 1.2)

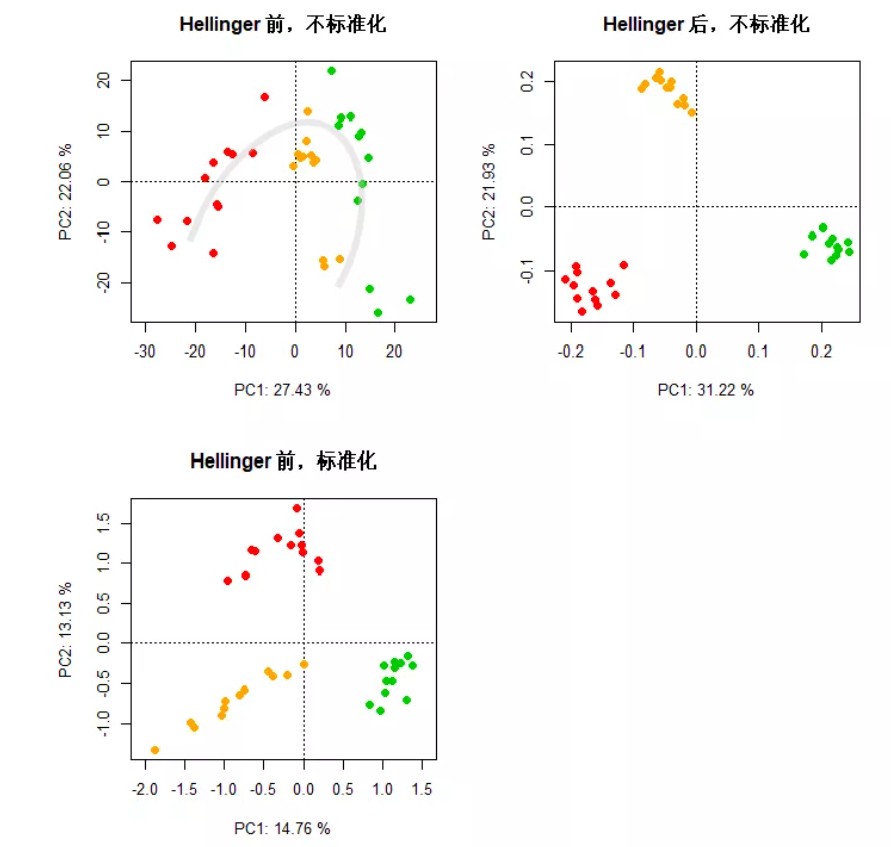
Hellinger转化前，且未标准化的数据，存在很大的方差、组内离散度高、趋势不明显且略微呈现了“马蹄形效应”；Hellinger转化后或者未Hellinger转化但标准化后的数据，样方分布明显，但相较之下，Hellinger转化后的区分程度更高，主成分轴的解释量具代表性。