排序分析PCA、PCoA、CA、NMDS、RDA、CCA等区别与联系
扩增子分析视频课程推荐:https://bdtcd.xet.tech/s/qZRiF
做微生物多样性研究的同学经常碰到各种降维排序分析方法,如PCA、PCOA、CA、DCA、NMDS、RDA、CCA等等。种类太多,对于新手来说很容易就搞混淆了,更别说考虑选哪一个方法更适合自己了。今天我就给大家介绍下各种方法的区别。
上述方法,主成分分析(PCA)、主坐标分析(PCOA)、对应分析(CA)、去趋势对应分析(DCA)和非度量多维尺度分析(NMDS)、冗余分析(RDA)、典范对应分析(CCA)都属于降维排序分析方法,其区别总结成一个表格如下:
distance based表示:特殊转换后的相异系数矩阵,bray curtis距离、Jaccard 距离,Unifrac距离矩阵
Raw dada based表示:输入的为不经转换的欧式距离
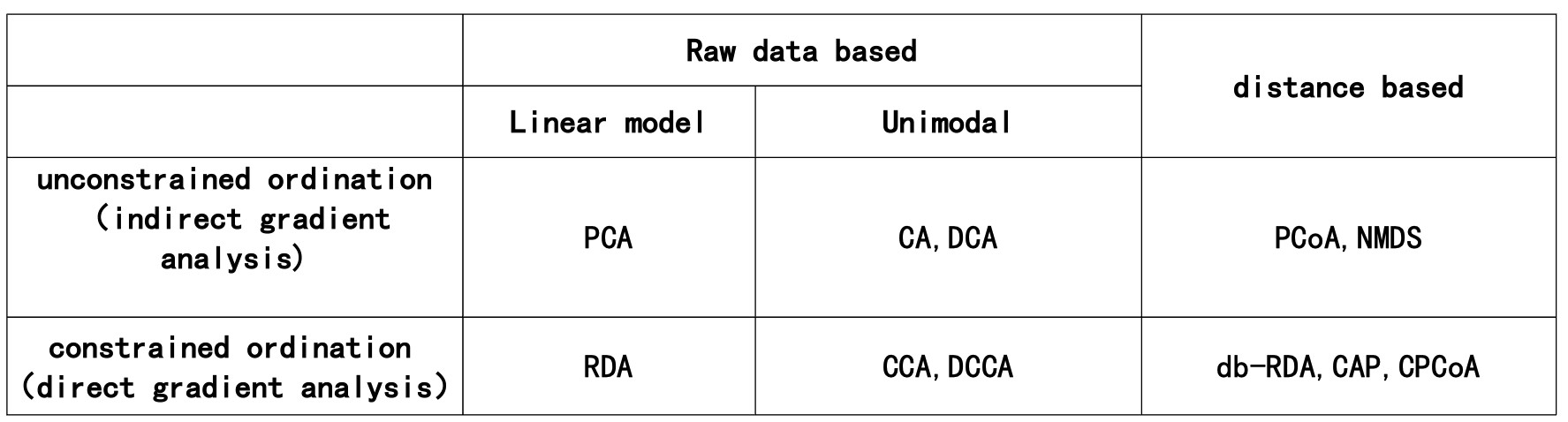
这里面牵涉到排序、降维排序、非约束排序和约束排序排序、线性模型和单峰模型等概念,下面我们就来一一讲解这些概念,相信看完之后您一定会对种类繁多的排序方法有了较为清晰的认识!什么是排序分析?
排序过程是将样品或物种排列在一定的空间,在一个低维空间中,使相似的样品或物种距离相近,相异的样品或物种距离较远。也就是说排序可以揭示微生物-环境间的生态关系,降低维数,减少坐标轴的数目,使排序轴能够反映一定的生态梯度。
为什么要做排序降维分析?
试想一下面对P(种)×N(样品)的原始数据矩阵(OTU table),即使是通过距离算法(欧式距离,jaccard距离,bray-curtis,unifrac距离等)得到两两样品之间的距离矩阵,也是N(样品)×N(样品)的大量数据,如果不借助任何统计方法,我们很难从这种多维的数据当中用肉眼观察到数据的内在关系,也就是微生物与环境的分布关系。
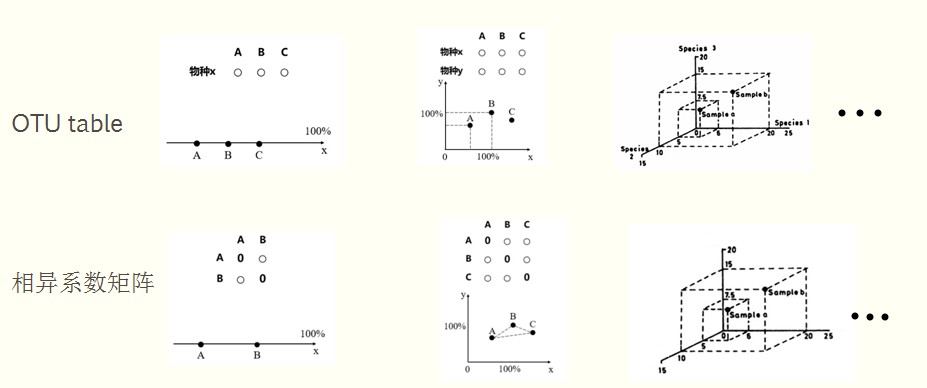
我们想用数据的可视化来展示我们的数据,如果输入的是OTU table的话,当样品较少,物种也较少的时候,我们可以将样品按照物种的丰度在多维空间上进行排序分布,如果是距离矩阵(不了解距离矩阵的看这里),可以得到两两样品的相异距离矩阵,我们可以利用相异矩阵在空间上排列样品,使样品在空间上的距离与原始的距离矩阵保持一致。如下图所示:
注:通过观察ABC三点之间的距离我们就能他们的之间的相异关系,距离越远相似性就越差,距离越近相似性就越高,
当然这里只举例了三维下的例子,再多的维度我也理解不了了。我们看到如果排序所用到的数据为OTU table的话,有多少个物种就有多少维空间,如果输入的是距离矩阵那么有n个样品,就有n-1个维度,最后的结果是数据还是非常复杂。排序降维意义
这时候又要用到排序降维的思想了,降维就是建立一个低维的空间,让原来多维的空间影射到这个低维的空间来,但让物种或样方空间关系失真最小。
降维的过程就像投影,找到最好的角度使投影后的物种或者样品的位置关系尽量保持原始的位置关系
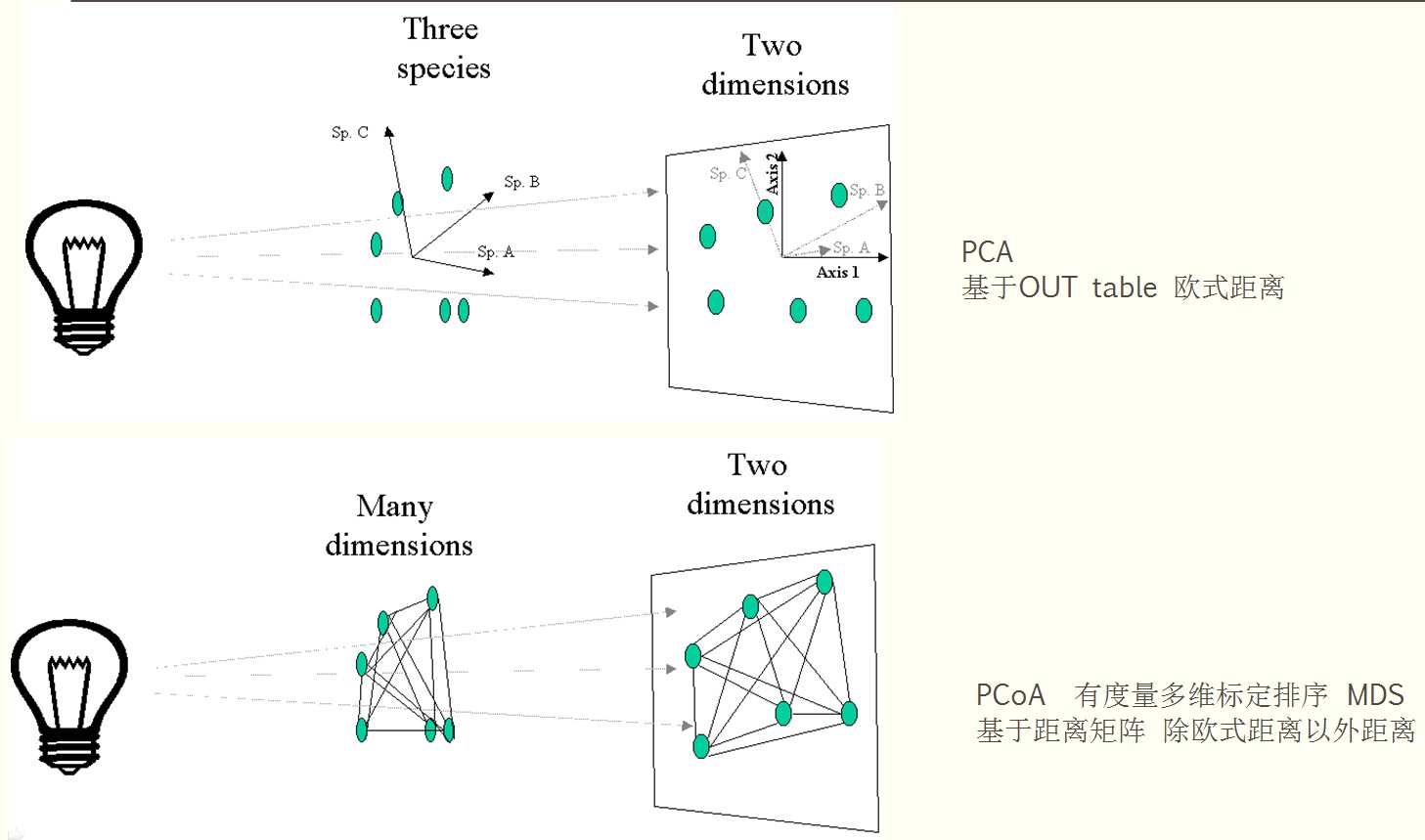
上面两个图分别代表了PCA的分析原理和PCoA的分析原理,不同之处是PCA是基于OTU table也就是基于欧式距离,而PCoA是基于两两样品之间的距离矩阵(前面提到的除欧式距离以外的其他距离矩阵),如果PCoA 也使用欧式距离矩阵的话,那么PCA和PCoA的分析结果是一样的。
另外,PCoA是基于距离矩阵,它的排序的目的是将N个样品排列在一定的空间,使得样品间的空间差异与原始距离矩阵保持一致,这类排序方法也称作多维标定排序(Multi—dimensional scaling)。如果排序依赖于相异系数的数值,就叫有度量多维标定法(metric multi—dimensional scaling)所以说PCoA分析也叫有度量多维标定法;如果排序仅仅决定于相异系数的大小顺序(秩次排序),则称为无度量多维标定法(Non—Metric Multi—Dimensional Scaling;NMDS)。评价 NMDS排序好坏的stress 值解释:在m维空间内构建对象的初始结构,初始结构是调整对象之间位置关系的起点;在m维空间内,用一个迭代程序不断调整对象位置,目标是不断最小化应力函数(Stress function,其值被转化为0~1间的数值,可以检验 NMDS 分析结果的优劣。通常认为 stress<0.2 时可用 NMDS 的二维点图表示,其图形有一定的解释意义;当 stress<0.1 时,可认为是一个好的排序;当 stress<0.05 时,则具有很好的代表性)不断调整对象位置,直至应力函数值不再减少,或已达到预定的值;
作者:生态数据
链接:https://www.jianshu.com/p/6bb937864b23
来源:简书
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
非约束排序和约束排序排序区别
非约束排序也叫间接梯度分析(unconstrained ordination or indirect gradient analysis)的目标就是发现这样的坐标轴,让群落中的样方或是物种的最大变化量能够在坐标轴上体现出来。换句话说,让尽可能多的变化量能够在尽可能少的轴上展示出来,并且让样方或物种在排序图能够可视化展示出来。当然,我们会经常期望这些轴能够代表一些潜在的环境变量。而约束排序(constrained ordination)的目的就是发现物种在环境梯度上的变化情况。说白了非约束排序不需要输入环境变量信息(如 PH,湿度,温度等),而约束排序需要环境信息,对排序图进行约束。典型的非约束排序有PCA,PCoA,NMDS,CA分析等,约束排序典型例子有RDA CCA等分析;其中RDA就是PCA的约束排序版本,CCA是CA分析对应的约束排序分析方法。
线性模型和单峰模型
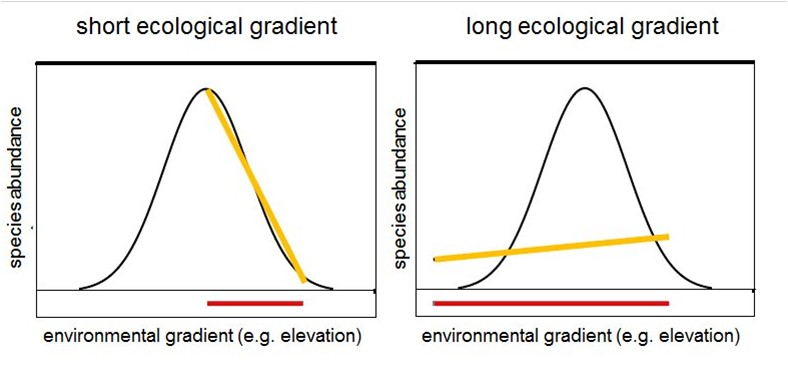
所有排序方法都是基于一定的模型之上,这种模型反映物种和环境之间的关系以及在某一环境梯度上的种间关系。最常用的关系模型有两种:一种是线形模型(linear model),另一种是单峰模型(unimodal model)。线形模型的含义表示某个植物种随着某一环境因子的变化而呈线性变化或叫线性响应(linear response)。单峰模型的含义是某个植物种的个体数随某个环境因子值的增加而增加。当环境因子增加到某一值时,植物种的个体数达到最大值,此时的环境因子值称为该种的最适值(optimum);随后当环境因子值继续增加时,种的个体数逐渐下降。为了简化单峰模型,我们经常假设单峰曲线以峰值为中心,两边是对称的。
CA
分析存在弓形效应
对应分析(Correspondence Analysis,CA,或称Reciprocal Averaging,RA),是一种单峰非约束排序方法,在生态学数据分析中常使用它计算样方与物种之间的对应关系。排序空间中,样方或物种之间的距离用χ2距离表示,与PCA(代表了欧几里得距离)相比,该距离测度不受双零问题的限制(但受稀有物种的影响较大)。用于CA的数据必须是频度或类频度、同量纲的非负数据。就群落排序而言,对应分析比主成分分析(PCA)更好,更稳健,但是在处理长生态梯度时存在缺陷或者“错误”,这些问题可以通过消除趋势的对应分析(Detrended Correspondence Analysis, DCA)处理。由于在对应分析(Correspondence analysis,CA)中可能会产生“弓形效应(arch effect)”,对排序的精度产生影响,与此对应,在CA的基础上衍生了去趋势对应分析(Detrended Correspondence Analysis,DCA)以解决这个问题。
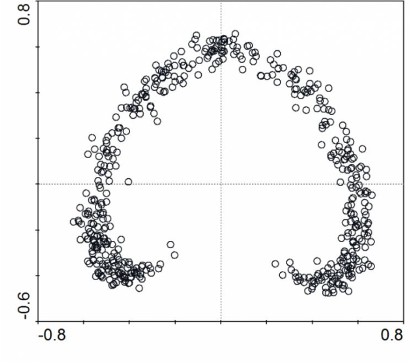
最左与最右不是最远,反而是最近
排序分析选择
进行排序分析之前,首先要判断是选择线性模型(PCA 和RDA)还是单峰模型(CA和CCA)的排序方法。一般来说,如果物种分布变化大或者环境梯度变化大(多为自然环境取样环境变化梯度较大),选择单峰模型效果比较好,反之,选择线性模型,虽然单峰模型可以包括线性模型,但是线性模型会更精确,如上图左图。自己判断环境变化还是太主观,我们可以通过DCA分析来判断,如果DCA排序前4个轴中最大值超过4,选择单峰模型排序更合适。如果是小于3,则选择线性模型更好(Lepx & Smilauer 2003)。如果介于3-4之间,单峰模型和线性模型都可行。
注:单峰模型可以包含线性模型参考资料:
[1] http://ordination.okstate.edu/overview.htm
[2] 数量生态学-张金屯.pdf
[3] 基于CANOCO的生态学数据的多元统计分析排序分析PCA等.pdf
想获取以上资料的同学可以转发本微信稿到朋友圈,并截图回复到我们公众号,然后回复:"微生态" 关键字,就可以获得以上资料。
推荐课程:微生物扩增子分析课程实操
更多生物信息课程:https://study.omicsclass.com/index
- 发表于 2018-05-29 13:00
- 阅读 ( 41920 )
- 分类:宏基因组
你可能感兴趣的文章
- 典型相关性分析CCA与冗余分析RDA 9937 浏览
- 跟着文献学做图 | 用蛋白质序列做主成分分析(PCA) 4787 浏览
- 使用DNA序列做主成分分析(PCA)——R语言adegenet包 5719 浏览
- 主成分分析(PCA)如何计算方差解释率 8531 浏览
- 群体遗传进化PCA分析 3200 浏览
- PCAI型标尺与II型标尺 4847 浏览

