层次聚类方法详解
聚类算法综述
聚类分析(clustering analysis)是将一组对象根据其特征分成不同的 cluster,使得同一 cluster 内的对象在某种意义上比不同的 cluster 之间的对象更为相似。
由于 “cluster” 没有一个明确的定义,因而会有基于不同的模型的聚类算法,其中被广泛运用的聚类算法有以下几类:
- 基于连通模型(connectivity-based)的聚类算法: 即本文将要讲述的层次聚类算法,其核心思想是按照对象之间的距离来聚类,两个离的近的对象要比两个离的远的对象更有可能属于同一 cluster。
- 基于中心点模型(centroid-based)的聚类算法: 在此类算法中,每个 cluster 都维持一个中心点(centorid),该中心点不一定属于给定的数据集。当预先指定聚类数目 k 时,此类算法需要解决一个优化问题,目标函数为所有的对象距其所属的 cluster 的中心点的距离的平方和,优化变量为每个 cluster 的中心点以及每个对象属于哪个 cluster;此优化问题被证明是 NP-hard 的,但有一些迭代算法可以找到近似解,k-means 算法 即是其中的一种。
- 基于分布模型(distribution-based)的聚类算法: 此类算法认为数据集中的数据是由一种混合概率模型所采样得到的,因而只要将可能属于同一概率分布所产生的数据归为同一 cluster 即可,最常被使用的此类算法为 高斯混合模型(GMM)聚类。
- 基于密度(density-based)的聚类算法: 在此类算法中,密度高的区域被归为一个 cluster,cluster 之间由密度低的区域隔开,密度低的区域中的点被认为是噪声 (noise),常用的密度聚类算法为 DBSCAN 和 OPTICS。
层次聚类综述
层次聚类算法 (hierarchical clustering) 将数据集划分为一层一层的 clusters,后面一层生成的 clusters 基于前面一层的结果。层次聚类算法一般分为两类:
- Agglomerative 层次聚类:又称自底向上(bottom-up)的层次聚类,每一个对象最开始都是一个 cluster,每次按一定的准则将最相近的两个 cluster 合并生成一个新的 cluster,如此往复,直至最终所有的对象都属于一个 cluster。本文主要关注此类算法。
- Divisive 层次聚类: 又称自顶向下(top-down)的层次聚类,最开始所有的对象均属于一个 cluster,每次按一定的准则将某个 cluster 划分为多个 cluster,如此往复,直至每个对象均是一个 cluster。
下图直观的给出了层次聚类的思想以及以上两种聚类策略的异同。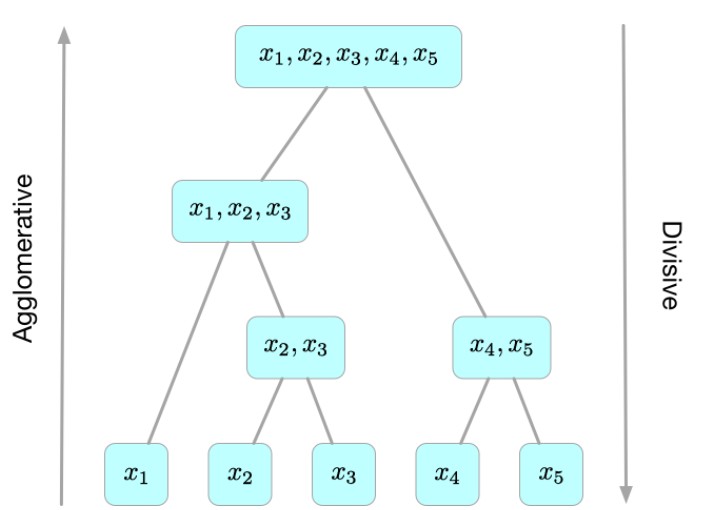
另外,需指出的是,层次聚类算法是一种贪心算法(greedy algorithm),因其每一次合并或划分都是基于某种局部最优的选择。
树形图
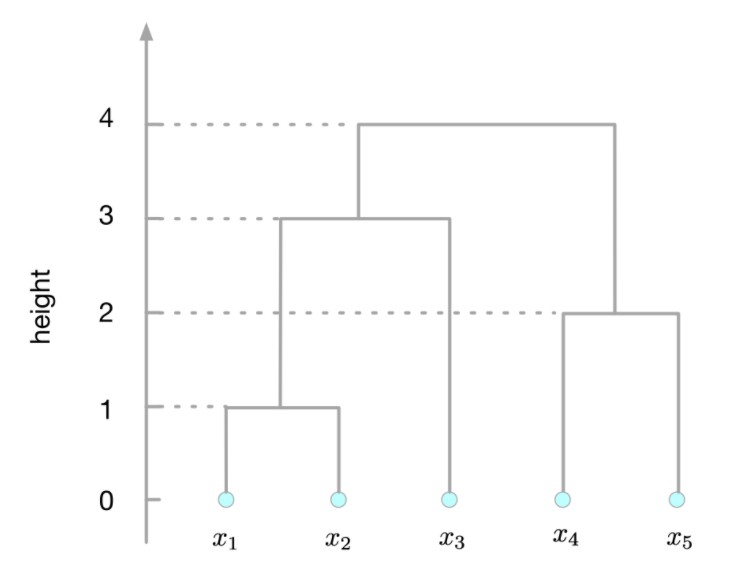
树形图 (dendrogram)可以用来直观地表示层次聚类的成果。一个有 5 个点的树形图如下图所示,其中纵坐标高度表示不同的 cluster 之间的距离(“距离”的衡量准则可以多种多样,详见本文后面的定义),可以从这张图看到,x1x1 和 x2x2 的距离最近(为 1),因此将 x1x1 和 x2x2 合并为一个 cluster (x1,x2)(x1,x2),所以在树形图中首先将节点 x1x1 和 x2x2 连接,使其成为一个新的节点 (x1,x2)(x1,x2) 的子节点,并将这个新的节点的高度置为 1;之后再在剩下的 4 个 cluster (x1,x2)(x1,x2), x3x3, x4x4 和 x5x5 中选取距离最近的两个 cluster 合并,x4x4 和 x5x5 的距离最近(为 2),因此将 x4x4 和 x5x5 合并为一个 cluster (x4,x5)(x4,x5),体现在树形图上,是将节点 x4x4 和 x5x5 连接,使其成为一个新的节点 (x4,x5)(x4,x5) 的子节点,并将此新节点的高度置为 2;….依此模式进行树形图的生成,直至最终只剩下一个 cluster ((x1,x2),x3),(x4,x5))((x1,x2),x3),(x4,x5))。
可以直观地看到,如果我们想得到一个聚类结果,使任意的两个 cluster 之间的距离都不大于 hh,我们只要在树形图上作一条水平的直线对其进行切割,使其纵坐标等于 hh,即可获得对应的聚类结果。例如,在下面的树形图中,设 h=2.5h=2.5,即可得到 3 个 cluster (x1,x2)(x1,x2), x3x3 和 (x4,x5)(x4,x5)。
对象之间的距离衡量
衡量两个对象之间的距离的方式有多种,对于数值类型(Numerical)的数据,常用的距离衡量准则有 Euclidean 距离、Manhattan 距离、Chebyshev 距离、Minkowski 距离等等。对于 dd 维空间的两个对象 x=[x1,x2,…,xd]Tx=[x1,x2,…,xd]T 和 y=[y1,y2,…,yd]Ty=[y1,y2,…,yd]T,其在不同距离准则下的距离计算方法如下表所示:
| Euclidean 距离 | d(x,y)=[∑dj=1(xj−yj)2]12=[(x−y)T(x−y)]12d(x,y)=[∑j=1d(xj−yj)2]12=[(x−y)T(x−y)]12 |
| Manhattan 距离 | d(x,y)=∑dj=1∣xj−yj∣d(x,y)=∑j=1d∣xj−yj∣ |
| Chebyshev 距离 | d(x,y)=max1≤j≤d∣xj−yj∣d(x,y)=max1≤j≤d∣xj−yj∣ |
| Minkowski 距离 | d(x,y)=[∑dj=1(xj−yj)p]1p,p≥1d(x,y)=[∑j=1d(xj−yj)p]1p,p≥1 |
Minkowski 距离就是 LpLp 范数(p≥1p≥1),而 Manhattan 距离、Euclidean 距离、Chebyshev 距离分别对应 p=1,2,∞p=1,2,∞ 时的情形。
另一种常用的距离是 Maholanobis 距离,其定义如下:
其中 ΣΣ 为数据集的协方差矩阵,为给出协方差矩阵的定义,我们先给出数据集的一些设定,假设数据集为 X=(x1,x2,…,xn)∈Rd×nX=(x1,x2,…,xn)∈Rd×n,xi∈Rdxi∈Rd 为第 ii 个样本点,每个样本点的维度为 dd,样本点的总数为 nn 个;再假设样本点的平均值 mx=1n∑ni=1ximx=1n∑i=1nxi 为 00 向量(若不为 00,我们总可以将每个样本都减去数据集的平均值以得到符合要求的数据集),则协方差矩阵 Σ∈Rd×dΣ∈Rd×d 可被定义为
Maholanobis 距离不同于 Minkowski 距离,后者衡量的是两个对象之间的绝对距离,其值不受数据集的整体分布情况的影响;而 Maholanobis 距离则衡量的是将两个对象置于整个数据集这个大环境中的一个相异程度,两个绝对距离较大的对象在一个分布比较分散的数据集中的 Maholanobis 距离有可能会比两个绝对距离较小的对象在一个分布比较密集的数据集中的 Maholanobis 距离更小。更细致地来讲,Maholanobis 距离是这样计算得出的:先对数据进行主成分分析,提取出互不相干的特征,然后再将要计算的对象在这些特征上进行投影得到一个新的数据,再在这些新的数据之间计算一个加权的 Euclidean 距离,每个特征上的权重与该特征在数据集上的方差成反比。由这些去相干以及归一化的操作,我们可以看到,对数据进行任意的可逆变换,Maholanobis 距离都保持不变。
Cluster 之间的距离衡量
除了需要衡量对象之间的距离之外,层次聚类算法还需要衡量 cluster 之间的距离,常见的 cluster 之间的衡量方法有 Single-link 方法、Complete-link 方法、UPGMA(Unweighted Pair Group Method using arithmetic Averages)方法、WPGMA(Weighted Pair Group Method using arithmetic Averages)方法、Centroid 方法(又称 UPGMC,Unweighted Pair Group Method using Centroids)、Median 方法(又称 WPGMC,weighted Pair Group Method using Centroids)、Ward 方法。前面四种方法是基于图的,因为在这些方法里面,cluster 是由样本点或一些子 cluster (这些样本点或子 cluster 之间的距离关系被记录下来,可认为是图的连通边)所表示的;后三种方法是基于几何方法的(因而其对象间的距离计算方式一般选用 Euclidean 距离),因为它们都是用一个中心点来代表一个 cluster 。假设 CiCi 和 CjCj 为两个 cluster,则前四种方法定义的 CiCi 和 CjCj 之间的距离如下表所示:
| Single-link | D(Ci,Cj)=minx∈Ci,y∈Cjd(x,y)D(Ci,Cj)=minx∈Ci,y∈Cjd(x,y) |
| Complete-link | D(Ci,Cj)=maxx∈Ci,y∈Cjd(x,y)D(Ci,Cj)=maxx∈Ci,y∈Cjd(x,y) |
| UPGMA | D(Ci,Cj)=1∣Ci∣∣Cj∣∑x∈Ci,y∈Cjd(x,y)D(Ci,Cj)=1∣Ci∣∣Cj∣∑x∈Ci,y∈Cjd(x,y) |
| WPGMA | omitting |
其中 Single-link 定义两个 cluster 之间的距离为两个 cluster 之间距离最近的两个对象间的距离,这样在聚类的过程中就可能出现链式效应,即有可能聚出长条形状的 cluster;而 Complete-link 则定义两个 cluster 之间的距离为两个 cluster 之间距离最远的两个对象间的距离,这样虽然避免了链式效应,但其对异常样本点(不符合数据集的整体分布的噪声点)却非常敏感,容易产生不合理的聚类;UPGMA 正好是 Single-link 和 Complete-link 的一个折中,其定义两个 cluster 之间的距离为两个 cluster 之间两个对象间的距离的平均值;而 WPGMA 则计算的是两个 cluster 之间两个对象之间的距离的加权平均值,加权的目的是为了使两个 cluster 对距离的计算的影响在同一层次上,而不受 cluster 大小的影响(其计算方法这里没有给出,因为在运行层次聚类算法时,我们并不会直接通过样本点之间的距离之间计算两个 cluster 之间的距离,而是通过已有的 cluster 之间的距离来计算合并后的新的 cluster 和剩余 cluster 之间的距离,这种计算方法将由下一部分中的 Lance-Williams 方法给出)。
Centroid/UPGMC 方法给每一个 cluster 计算一个质心,两个 cluster 之间的距离即为对应的两个质心之间的距离,一般计算方法如下:
- 发表于 2021-06-22 17:26
- 阅读 ( 3157 )
- 分类:其他
你可能感兴趣的文章
相关问题
0 条评论
发送私信
举报此文章
如果觉得我的文章对您有用,请随意打赏。你的支持将鼓励我继续创作!
