R语言基础入门—数据结构（1）
R语言作为生信分析最常用的编程语言之一，经常被用于进行生物数据统计分析和绘图。之前小编给大家介绍了R语言下载安装和一些基础概念，今天继续介绍R语言的数据结构。
R语言数据结构包括向量，矩阵和数据框，数组， 列表，因子等，主要是线性代数中的一些概念。
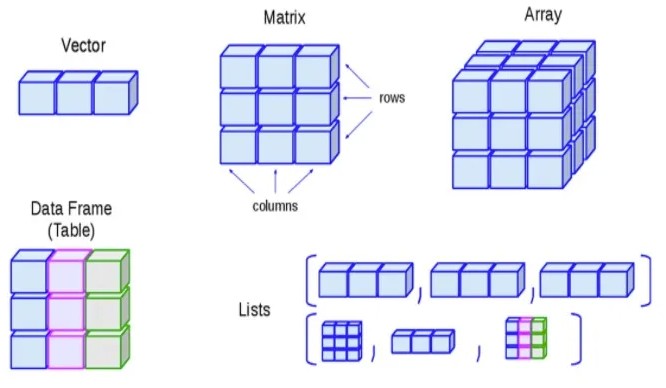
向量
向量是最基本的R数据对象，有六种类型的原子向量。它们分别是逻辑型（logical），整型（integer），双精度型（double），字符型（character），复数型（complex）和原始型（raw）。
创建向量
即使在R中只写入一个值，它也会被认为是一个长度为1的向量，以下我们创建单个元素的向量，可以是以上 6 中类型中的任意一种：
# 字符型原子向量
print("runoob");
# 双精度型原子向量
print(12.5)
# 整型原子向量
print(23L)
# 逻辑型原子向量
print(TRUE)
# 复数型原子向量
print(2+3i)
# 原始型原子向量
print(charToRaw('hello'))
执行以上代码输出结果为：
[1] "runoob"
[1] 12.5
[1] 23
[1] TRUE
[1] 2+3i
[1] 68 65 6c 6c 6f
以下我们创建多个元素的向量，数字之间使用冒号 ":" 运算符：
# 创建 5 到 13 到系列
v <- 5:13
print(v)
# 创建 6.6 到 12.6 的系列
v <- 6.6:12.6
print(v)
# 如果最后一个元素不属于系列，就丢弃
v <- 3.8:11.4
print(v)
执行以上代码输出结果为：
[1] 5 6 7 8 9 10 11 12 13
[1] 6.6 7.6 8.6 9.6 10.6 11.6 12.6
[1] 3.8 4.8 5.8 6.8 7.8 8.8 9.8 10.8
我们也可以使用系列运算符 seq() 来创建向量。
#创建 5 到 9 递增 0.4 的向量：
print(seq(5, 9, by = 0.4))
执行以上代码输出结果为：
[1] 5.0 5.4 5.8 6.2 6.6 7.0 7.4 7.8 8.2 8.6 9.0
使用c()函数创建向量，如果其中一个元素是字符，则非字符值被强制为字符类型。
# 数字和逻辑字符将转化为字符类型
s <- c('apple','red',5,TRUE)
print(s)
执行以上代码输出结果为：
[1] "apple" "red" "5" "TRUE"
访问向量元素
访问向量元素可以使用中括号 []，索引值从 1 开始（跟其他编程语言不太一样），如果索引为负数，则会删除该位置的元素，TRUE，FALSE 或 0 和 1。
# 使用索引访问向量元素
t <- c("Sun","Mon","Tue","Wed","Thurs","Fri","Sat")
u <- t[c(2,3,6)]
print(u)
# 使用逻辑索引，TRUE 表示读取，FALSE 为不读取
v <- t[c(TRUE,FALSE,FALSE,FALSE,FALSE,TRUE,FALSE)]
print(v)
# 第二个和第五个会被删除
x <- t[c(-2,-5)]
print(x)
# 使用 0/1 索引，1 表示读取，0 为不读取
y <- t[c(0,0,0,0,0,0,1)]
print(y)
执行以上代码输出结果为：
[1] "Mon" "Tue" "Fri"
[1] "Sun" "Fri"
[1] "Sun" "Tue" "Wed" "Fri" "Sat"
[1] "Sat"
向量运算
我们可以对两个长度相同的向量进行相加，相减，相乘或相除等操作，结果同样以向量输出。
# 创建两个向量
v1 <- c(3,1,4,5,0,12)
v2 <- c(5,11,9,8,1,22)
# 相加
add.result <- v1+v2
print(add.result)
# V相减
sub.result <- v1-v2
print(sub.result)
# 相乘
multi.result <- v1*v2
print(multi.result)
# 相除
divi.result <- v1/v2
print(divi.result)
执行以上代码输出结果为：
[1] 8 12 13 13 1 34
[1] -2 -10 -5 -3 -1 -10
[1] 15 11 36 40 0 264
[1] 0.60000000 0.09090909 0.44444444 0.62500000 0.00000000 0.54545455
循环向量
如果两个元素的向量长度不一样，较短的会循环自身的元素，直到与长的向量元素一致。
v1 <- c(1,8,7,5,0,12)
v2 <- c(5,6)
# V2 变成 c(5,6,5,6,5,6)
add.result <- v1+v2
print(add.result)
sub.result <- v1-v2
print(sub.result)
执行以上代码输出结果为：
[1] 6 14 12 11 5 18 [1] -4 2 2 -1 -5 6
向量排序
我们可以使用 sort() 函数对向量进行排序：
v <- c(2,11,6,5,0,21, -7, 111)
# 排序
sort.result <- sort(v)
print(sort.result)
# decreasing 参数 TRUE 设置为降序，默认为 FALSE 为升序
revsort.result <- sort(v, decreasing = TRUE)
print(revsort.result)
# 对字符类型进行排序
v <- c("Runoob","Google","Zhihu","Facebook")
sort.result <- sort(v)
print(sort.result)
# 降序
revsort.result <- sort(v, decreasing = TRUE)
print(revsort.result)
执行以上代码输出结果为：
[1] -7 0 2 5 6 11 21 111
[1] 111 21 11 6 5 2 0 -7
[1] "Facebook" "Google" "Runoob" "Zhihu"
[1] "Zhihu" "Runoob" "Google" "Facebook"
矩阵
矩阵是其中元素以二维矩形布局布置的R对象， 它们包含相同原子类型的元素。这种数据结构很类似于其它语言中的二维数组，但 R 提供了语言级的矩阵运算支持。
矩阵里的元素可以是数字、符号或数学式。
一个 M x N 的矩阵是一个由 M（row） 行 和 N 列（column）元素排列成的矩形阵列。
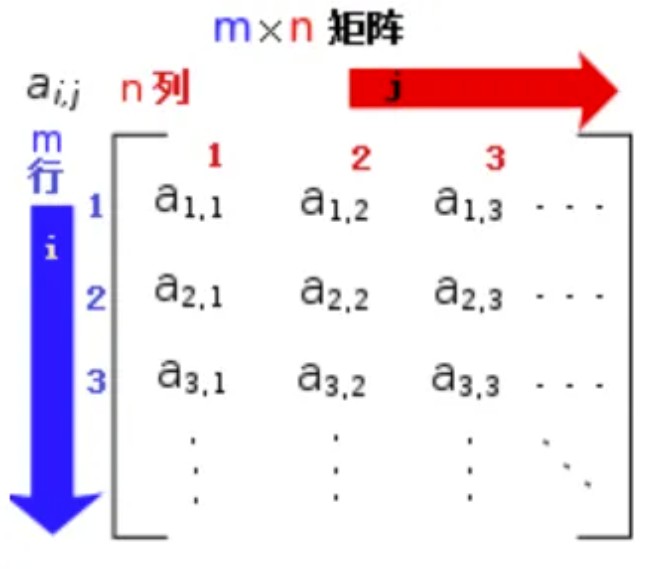
以下是一个由 6 个数字元素构成的 2 行 3 列的矩阵：
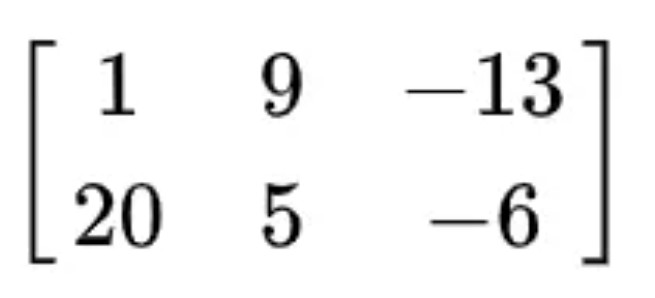
矩阵创建
R 语言的矩阵可以使用 matrix() 函数来创建，语法格式如下：
matrix(data = NA, nrow = 1, ncol = 1, byrow = FALSE,dimnames = NULL)
参数说明：
data 向量，矩阵的数据
nrow 行数
ncol 列数
byrow 逻辑值，为 FALSE 按列排列，为 TRUE 按行排列
dimname 设置行和列的名称
创建一个数字矩阵：
# byrow 为 TRUE 元素按行排列
M <- matrix(c(3:14), nrow = 4, byrow = TRUE)
print(M)
# Ebyrow 为 FALSE 元素按列排列
N <- matrix(c(3:14), nrow = 4, byrow = FALSE)
print(N)
# 定义行和列的名称
rownames = c("row1", "row2", "row3", "row4")
colnames = c("col1", "col2", "col3")
P <- matrix(c(3:14), nrow = 4, byrow = TRUE, dimnames = list(rownames, colnames))
print(P)
执行以上代码输出结果为：
[,1] [,2] [,3]
[1,] 3 4 5
[2,] 6 7 8
[3,] 9 10 11
[4,] 12 13 14
[,1] [,2] [,3]
[1,] 3 7 11
[2,] 4 8 12
[3,] 5 9 13
[4,] 6 10 14
col1 col2 col3
row1 3 4 5
row2 6 7 8
row3 9 10 11
row4 12 13 14
转置矩阵
R 语言矩阵提供了 t() 函数，可以实现矩阵的行列互换。
例如有个 m 行 n 列的矩阵，使用 t() 函数就能转换为 n 行 m 列的矩阵。
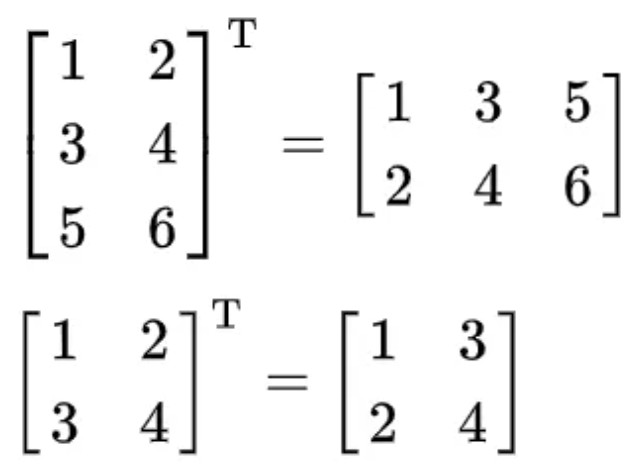
# 创建一个 2 行 3 列的矩阵
M = matrix( c(2,6,5,1,10,4), nrow = 2,ncol = 3,byrow = TRUE)
print(M)
# 转换为 3 行 2 列的矩阵
print(t(M))
执行以上代码输出结果为：
[,1] [,2] [,3]
[1,] 2 6 5
[2,] 1 10 4
"-----转置后-----"
[,1] [,2]
[1,] 2 1
[2,] 6 10
[3,] 5 4
矩阵有一个dim属性，内容是两个元素的向量， 两个元素分别为矩阵的行数和列数。dim属性可以用dim()函数访问。如:
# 创建一个 2 行 3 列的矩阵
M = matrix( c(2,6,5,1,10,4), nrow = 2,ncol = 3,byrow = TRUE)
print(M)
[,1] [,2] [,3]
[1,] 2 6 5
[2,] 1 10 4
dim(A)
[1] 2 3
访问矩阵元素
如果想获取矩阵元素，可以通过使用元素的列索引和行索引，类似坐标形式。
# 定义行和列的名称
rownames = c("row1", "row2", "row3", "row4")
colnames = c("col1", "col2", "col3")
# 创建矩阵
P <- matrix(c(3:14), nrow = 4, byrow = TRUE, dimnames = list(rownames, colnames))
print(P)
# 获取第一行第三列的元素
print(P[1,3])
# 获取第四行第二列的元素
print(P[4,2])
# 获取第二行
print(P[2,])
# 获取第三列
print(P[,3])
执行以上代码输出结果为：
col1 col2 col3
row1 3 4 5
row2 6 7 8
row3 9 10 11
row4 12 13 14
[1] 5
[1] 13
col1 col2 col3
6 7 8
row1 row2 row3 row4
5 8 11 14
矩阵计算
大小相同（行数列数都相同）的矩阵之间可以相互加减，具体是对每个位置上的元素做加减法。矩阵的乘法则较为复杂。两个矩阵可以相乘，当且仅当第一个矩阵的列数等于第二个矩阵的行数。
矩阵加减法
# 创建 2 行 3 列的矩阵
matrix1 <- matrix(c(7, 9, -1, 4, 2, 3), nrow = 2)
print(matrix1)
matrix2 <- matrix(c(6, 1, 0, 9, 3, 2), nrow = 2)
print(matrix2)
# 两个矩阵相加
result <- matrix1 + matrix2
cat("相加结果：","\n")
print(result)
# 两个矩阵相减
result <- matrix1 - matrix2
cat("相减结果：","\n")
print(result)
执行以上代码输出结果为：
[,1] [,2] [,3]
[1,] 7 -1 2
[2,] 9 4 3
[,1] [,2] [,3]
[1,] 6 0 3
[2,] 1 9 2
相加结果：
[,1] [,2] [,3]
[1,] 13 -1 5
[2,] 10 13 5
相减结果：
[,1] [,2] [,3]
[1,] 1 -1 -1
[2,] 8 -5 1
矩阵乘除法
# 创建 2 行 3 列的矩阵
matrix1 <- matrix(c(7, 9, -1, 4, 2, 3), nrow = 2)
print(matrix1)
matrix2 <- matrix(c(6, 1, 0, 9, 3, 2), nrow = 2)
print(matrix2)
# 两个矩阵相乘
result <- matrix1 * matrix2
cat("相乘结果：","\n")
print(result)
# 两个矩阵相除
result <- matrix1 / matrix2
cat("相除结果：","\n")
print(result)
执行以上代码输出结果为：
[,1] [,2] [,3]
[1,] 7 -1 2
[2,] 9 4 3
[,1] [,2] [,3]
[1,] 6 0 3
[2,] 1 9 2
相乘结果：
[,1] [,2] [,3]
[1,] 42 0 6
[2,] 9 36 6
相除结果：
[,1] [,2] [,3]
[1,] 1.166667 -Inf 0.6666667
[2,] 9.000000 0.4444444 1.5000000
- 发表于 2024-11-12 17:50
- 阅读 ( 301 )
- 分类：R
