相关性分析作为一种强大的工具，能够帮助我们量化变量间的关联程度。R 语言中可以做相关性矩阵可视化的包有很多，小编最喜欢用的还是corrplot 这个包。

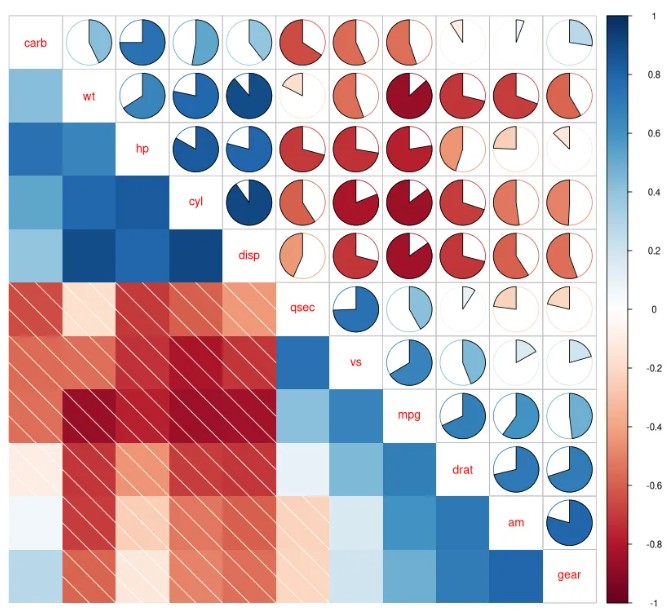
corrplot包非常容易使用，并在可视化方法、图形布局、颜色、图例、文本标签等方面提供了丰富的绘图参数。它还提供了p值和置信区间，以帮助用户确定相关的统计显著性。下面我们以转录组表达量数据为例，使用corrplot包绘制样品间的相关性图，绘图脚本如下：

1.加载需要的包

# 1.安装CRAN来源常用包
#设置镜像，
local({r <- getOption("repos")
r["CRAN"] <- "http://mirrors.tuna.tsinghua.edu.cn/CRAN/"
options(repos=r)})
# 依赖包列表：自动加载并安装
package_list <- c("dplyr","corrplot","RColorBrewer","devtools")
# 判断R包加载是否成功来决定是否安装后再加载
for(p in package_list){
  if(!suppressWarnings(suppressMessages(require(p, character.only = TRUE, quietly = TRUE, warn.conflicts = FALSE)))){
    install.packages(p,  warn.conflicts = FALSE)
    suppressWarnings(suppressMessages(library(p, character.only = TRUE, quietly = TRUE, warn.conflicts = FALSE)))
  }
}

2.读入数据

#设置工作路径
setwd("~/work/03.deg")
#读入数据
data<-read.table("fpkm.xls", header=TRUE,sep = "\t",check.names=FALSE,row.names=1)
head(data)

基因表达量数据格式如下：

ID      A1-1    A1-2    A1-3    B1-1    B1-2    B1-3    A2-1    A2-2    A2-3    B2-1    B2-2    B2-3
FtPinG0000001800.01     15.1995160901025        16.441577150186 17.2867772136153        20.0123886434312        20.5339961826528        21.030851469837 18.8867556381351       19.9059977192796        20.2262281764502        40.959707297525 36.2627040170818        36.2719103917479
FtPinG0000002000.01     8.97531375191129        9.11978258738736        9.85238719797644        8.84397160213807        9.66296609611642        9.56993910901853      10.7337560132642 10.6955187445875        10.174602368444 18.726301862827 19.744963523371 17.3371843121483
FtPinG0000002300.01     0.10096169501517        0.23839548136093        0.0854956827825154      0.37158122584763        0.199269668964403       0.295200470823108     0.0377515062095995       0.17911701881884        0.129515327078851       0.272975348387301       0.240196848553491       0.213872775624117
FtPinG0000002800.01     0.0691371370886746      0.16324984513874        0.268336893105438       0.0553159900786594      0.200672122973102       0.0594556165929241    0.14541579072095 0.2259467268409 0.155207954001583       0.116831029830459       0.0195813566486246      0.0228839131230015
FtPinG0000003000.01     488.861014449897        550.333645893939        442.444481899145        75.5380031354494        64.4440513891441        57.6249425862915      254.156489961737 256.297317496125        251.784160910779        32.0265556912271        32.5182736365053        35.4868859947427
FtPinG0000003200.01     22.6122074811821        22.9234651150848        22.1955511912947        13.1976268830233        13.9488878286769        14.5630548222237      26.260610275161  24.579965406508 24.5554860909515        19.374652724498 17.9159765083164        18.1895860061232
FtPinG0000011200.01     2.28786192141911        2.17588880489401        2.48900975204522        3.83895975408766        4.85130647216345        3.57972862781851      1.76738814933271 1.94341357417698        2.24194284443757        5.66495659137527        4.53585576331562        5.84777970567225
FtPinG0000011400.01     0       0       0       0       0       0       0       0       0       0       0       0
FtPinG0000011500.01     17.9584332209316        17.800309707057 19.4348761621419        12.1970372253972        12.2532093298866        11.3234221949391        18.5570812100419       19.6154291160033        18.4384954308382        13.8995891670914        14.5566151353016        13.1524676396182

3.数据处理

#使用spearman方法计算相关性
corr_matrix <- cor(data,method="spearman")
head(corr_matrix)

4.绘图

my_col<-colorRampPalette(c("yellow","orange","red"))
corrplot(corr_matrix,
         type = "upper",
         order = "AOE",      # 矩阵的排序方法，如 'original'、'AOE'、'hclust' 等
         is.corr = FALSE,    # 逻辑值，指示输入矩阵是否为相关性矩阵。
         col = my_col(100),  # 颜色向量，用于图形的颜色分布。
         col.lim = c(0.8,1), # 颜色分配的限制区间(相关性值区间)。
         tl.col = "black",   
         addCoef.col = "black",  # 添加相关系数
         number.cex = 0.7)       # 数字字体大小

结果如下图：

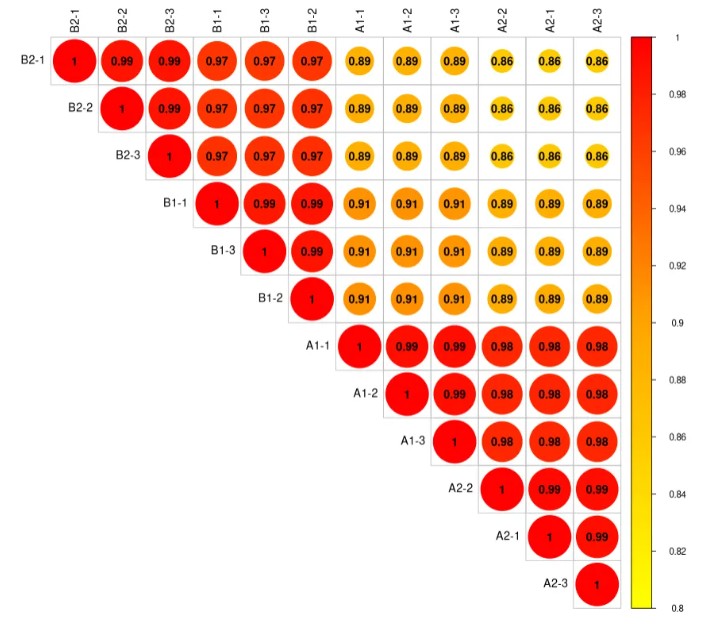
图形类型默认为圆形，将其改为矩形的：

corrplot(corr_matrix,method = 'square',
         type = "upper",
         order = "AOE",      # 矩阵的排序方法，如 'original'、'AOE'、'hclust' 等
         is.corr = FALSE,    # 逻辑值，指示输入矩阵是否为相关性矩阵。
         col = my_col(100),  # 颜色向量，用于图形的颜色分布。
         col.lim = c(0.8,1), # 颜色分配的限制区间(相关性值区间)。
         tl.col = "black",   
         addCoef.col = "black",  # 添加相关系数
         number.cex = 1)       # 数字字体大小

结果如下图：

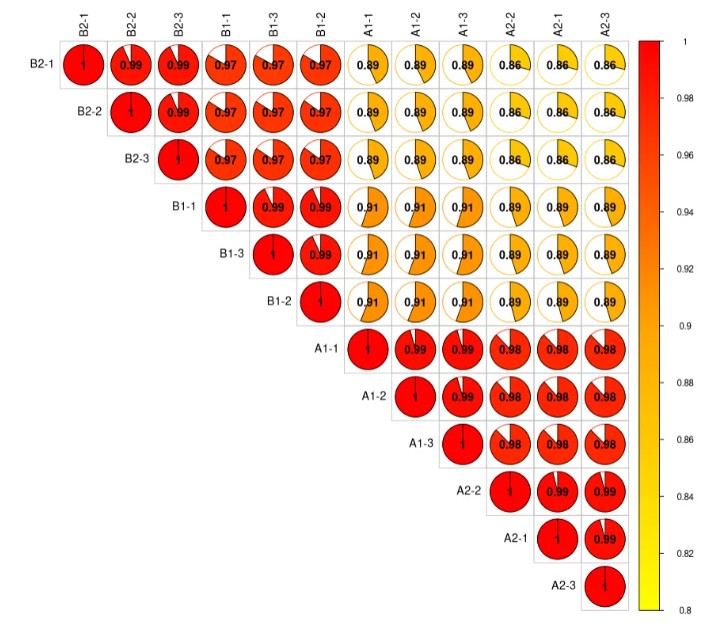
还可以修改为饼图：

corrplot(corr_matrix,method = 'pie',
         type = "upper",
         order = "AOE",      # 矩阵的排序方法，如 'original'、'AOE'、'hclust' 等
         is.corr = FALSE,    # 逻辑值，指示输入矩阵是否为相关性矩阵。
         col = my_col(100),  # 颜色向量，用于图形的颜色分布。
         col.lim = c(0.8,1), # 颜色分配的限制区间(相关性值区间)。
         tl.col = "black",   
         addCoef.col = "black",  # 添加相关系数
         number.cex = 1)       # 数字字体大小

结果如下图：

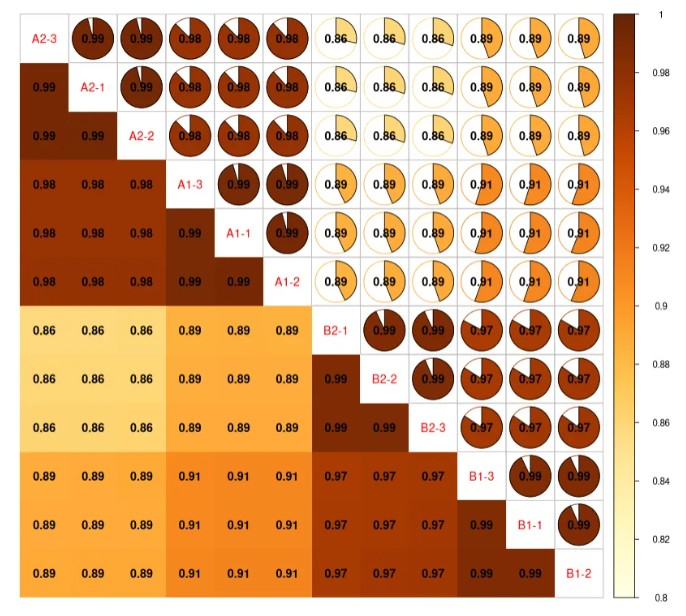
最后还可以合二为一：

corrplot.mixed(corr_matrix, 
              lower = 'shade', 
              upper = 'pie', 
              order = "AOE",      # 矩阵的排序方法，如 'original'、'AOE'、'hclust' 等
              is.corr = FALSE,    # 逻辑值，指示输入矩阵是否为相关性矩阵。
              col.lim = c(0.8,1), # 颜色分配的限制区间(相关性值区间)。
              addCoef.col = "black",  # 添加相关系数
              number.cex = 1)

结果如下图：

好了，小编就先给大家介绍到这里。希望对您的科研能有所帮助！祝您工作生活顺心快乐！