Beta多样性分析
Beta多样性用于不同生态系统之间多样性的比较,也就是样品间的差异,而上次提到的alpha多样性分析为样品内的多样性;Beta多样性利用各样本序列间的进化关系及丰度信息来计算样本间距离,反映样本(组)间是否具有显著的微生物群落差异。
Beta多样性计算
Beta多样性计算中主要基于OTU的群落比较方法,有欧式距离、bray curtis距离、Jaccard 距离,这些方法优势在于算法简单,考虑物种丰度(有无)和均度(相对丰度),但其没有考虑OTUs之间的进化关系,认为OTU之间不存在进化上的联系,每个OTU间的关系平等。
另一种算法Unifrac距离法,是根据系统发生树进行比较,会根据16s的序列信息对OTU进行进化树分类, 因此不同OTU之间的距离实际上有“远近”之分。
 注:UniFrac不能分析真菌
注:UniFrac不能分析真菌
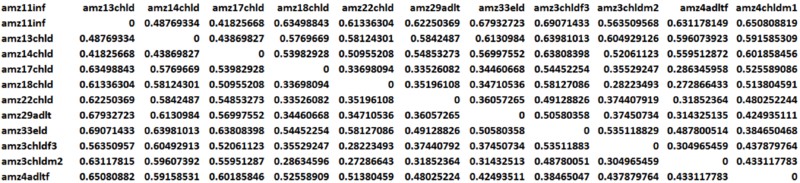
通过以上计算方法可以得到所有样品两两之间距离矩阵。这里重点说一下Unifrac距离矩阵:与欧式距离、bray curtis距离、Jaccard 距离不同,Unifrac距离矩阵又可分为weighted和Unweighted。其中Unweighted只考虑了物种有无的变化,因此结果中,0表示两个微生物群落间OTU的种类一致。而Weighted 则同时考虑物种有无和物种丰度的变化,结果中的0则表示群落间OTU的种类和数量都一致。
实际应用中 :在环境样本的检测中,由于影响因素复杂,群落间物种的组成差异更为剧烈,因此往往采用非加权方法进行分析。但如果要研究对照与实验处理组之间的关系,例如研究短期青霉素处理后,人肠道的菌落变化情况,由于处理后群落的组成一般不会发生大改变,但群落的丰度可能会发生大变化,因此更适合用加权方法去计算。基于这些相异矩阵可用于多种分析方法,下面主要介绍一下这些方法。
主成分分析PCA(Principal component analysis)是一种研究数据相似性或差异性的可视化方法,采取降维的思想,PCA 可以找到距离矩阵中最主要的坐标,把复杂的数据用一系列的特征值和特征向量进行排序后,选择主要的前几位特征值 ,来表示样品之间的关系。通过PCA 可以观察个体或群体间的差异。PC后面的百分数表示对应特征向量对数据的解释量,此值越大越好;
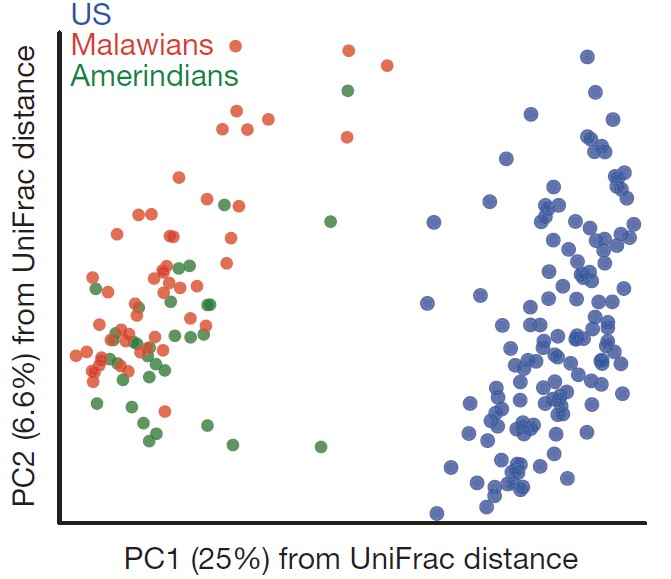 注:每一个点代表一个样本,相同颜色的点来自同一个分组,两点之间距离越近表明两者的群落构成差异越小。PCoA分析
注:每一个点代表一个样本,相同颜色的点来自同一个分组,两点之间距离越近表明两者的群落构成差异越小。PCoA分析
PCoA(principal co-ordinates analysis)主坐标分析法是一种与 PCA 类似的降维排序方法。PCoA与PCA的区别在于PCA是基于原始的物种组成矩阵所做的分析,使用的是欧式距离,仅仅比较的是物种丰度的不同,而PCoA首先根据不同的距离算法计算样品之间的距离(bray curtis距离、Jaccard 距离,Unifrac距离矩阵),然后对距离矩阵进行处理,使图中点间的距离正好等于原来的差异数据,实现定性数据的定量转换。百分比含义同PCA。
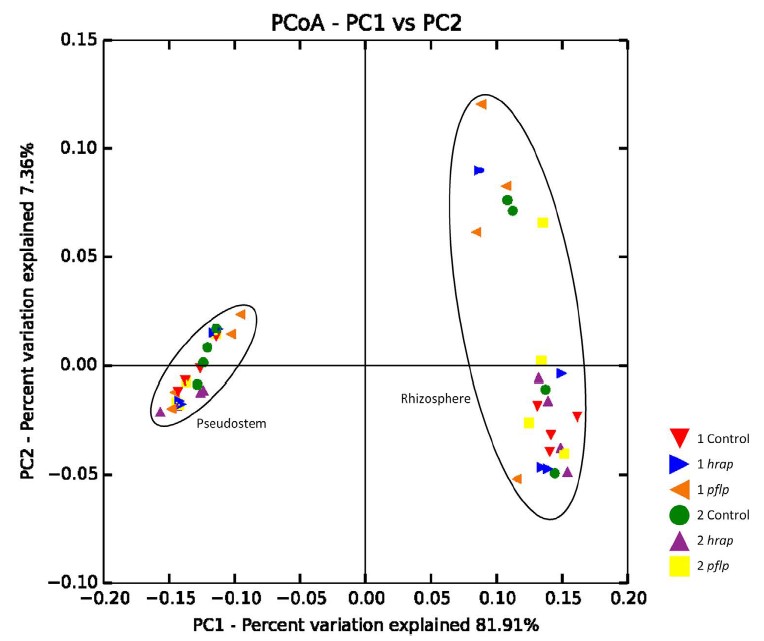 PCoA分析NMDS分析(非度量多维尺度分析)
PCoA分析NMDS分析(非度量多维尺度分析)
非度量多维标定法(Non-MetricMulti-Dimensional Scaling,NMDS)是一种适用于生态学研究的排序方法,主要是将多维空间的研究对象(样本或变量)简化到低维空间进行定位、分析和归类,同时又保留对象间原始关系的数据分析方法。类似于 PCA 或者 PCoA,通过样本的分布可以看出组间或组内差异。NMDS原设计的目的是为了克服以前排序方法中包括PCA、PCoA在内的缺点,即线性模型。NMDS的模型是非线性的,能更好地反映生态学数据的非线性结构,有的研究认为NMDS的效果优于PCA/PCoA。检验NMDS结果的优劣用胁迫系数(stress)来衡量,此值越小越好,当小于0.2是可以用NMDS的二维点图表示,当stress<0.05时具有很好的代表性:
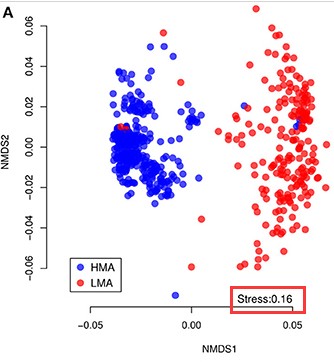 注:stress值越小越好UPGMA聚类分析
注:stress值越小越好UPGMA聚类分析
基于以上方法分析得到的距离矩阵,可用UPGMA(Unweighted Pair-group Method with Arithmetic Mean),分析样品间的差异。非加权组平均法,是一种常用的聚类分析方法。其原理是:假定的前条件是在进化过程中,每一世系发生趋异的次数相同,即核苷酸或氨基酸的替换速率是均等且恒定的。通过 UPGMA 法所产生的系统发生树,通过树枝的距离和聚类的远近可以观察样品间相似性。
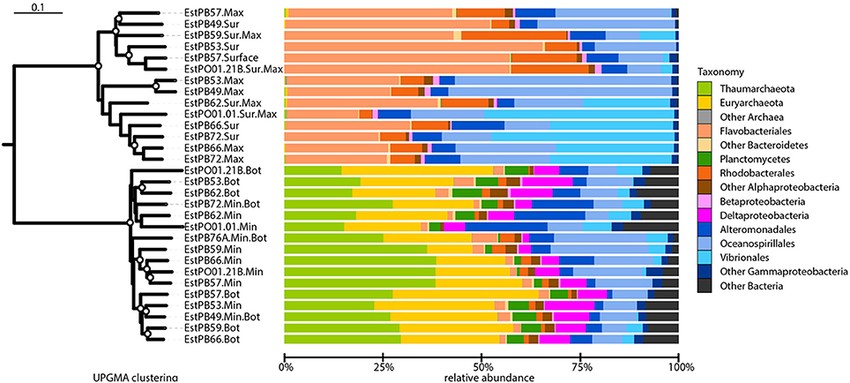 注:UPGMA聚类结果+样品相对丰度
注:UPGMA聚类结果+样品相对丰度
更多生物信息课程:https://study.omicsclass.com/index
- 发表于 2018-04-20 19:25
- 阅读 ( 19132 )
- 分类:宏基因组
你可能感兴趣的文章
- Root microbiota assembly and adaptive differentiation among European Arabidopsis populations 2897 浏览
- 微生物生态研究中常用数据库简介--转载 6404 浏览
- beta多样性中的距离矩阵总结 12808 浏览
- 微生物PCA分析和PCOA分析差别 21019 浏览
- 这种机器学习算法已经在微生物分析中成功应用 5490 浏览
相关问题
- 在进行物种累积丰度曲线时提醒没有该命令 1 回答
